
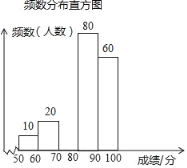
【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | n |
70≤x<80 | m | 0.15 |
80≤x<90 | 80 | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?
【答案】(1)m=30、n=0.1,补全图形如下见解析;(2)144°;(3)参加这次竞赛的1500名学生中成绩合格的大约有1050人.
【解析】
(1)由0.15×200求得m,由20÷200求得n;再根据求得的数据补全直方图;
(2)用360°×0.40即可得到答案;
(3)用成绩80分以上的频率(0.40+0.30)乘以总人数即可得到答案.
(1)m=0.15×200=30、n=20÷200=0.1,补全图形如下:
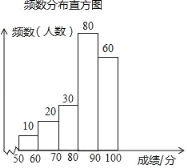
故答案为:30、0.1;
(2)分数段80≤x<90对应扇形的圆心角的度数是360°×0.40=144°,
故答案为:144°;
(3)参加这次竞赛的1500名学生中成绩合格的大约有1500×(0.40+0.30)=1050人.


科目:初中数学 来源: 题型:
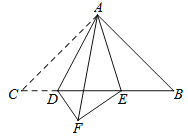
【题目】已知:如图,△ABC 中,∠CAB=90°,AC=AB,点 D、E 是 BC 上的两点,且∠DAE=45°,△ADC 与△ADF 关于直线AD 对称.
(1)求证:△AEF≌△AEB;
(2)求∠DFE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
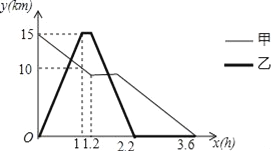
【题目】某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
(1)求甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式.
(2)求甲、乙第一次相遇的时间.
(3)直接写出乙回到侧门时,甲到侧门的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料;
课堂上,老师设计了一个活动:将一个4×4的正方形网格沿着网格线划分成两部分(分别用阴影和空白表示),使得这两部分图形是全等的,请同学们尝试给出划分的方法.约定:如果两位同学的划分结果经过旋转、翻折后能够重合,那么就认为他们的划分方法相同.
小方、小易和小红分别对网格进行了划分,结果如图①、图②、图③所示.
小方说:“我们三个人的划分方法都是正确的,但是将小红的整个图形(图③)逆时针旋转90![]() 后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同,”
后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同,”
老师说:“小方说得对.”

完成下列问题:
(1)图④的划分方法是否正确?
(2)判断图⑤的划分方法与图②小易的划分方法是否相同,并说明你的理由.
(3)请你再想出一种与已有方法不同的划分方法,使之满足上述条件,并在图⑥中画出来.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近端午节,某食品店每天卖出300只粽子,卖出一只粽子的利润为1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获得的利润更多,该店决定把零售单价下降m(0<m<1)元,
(1)零售单价降价后,每只利润为 元,该店每天可售出 只粽子.
(2)在不考虑其他因素的条件下,当零售单价下降多少元时,才能使该店每天获取的利润是420元,且卖出的粽子更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com