
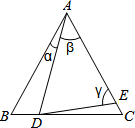
 如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )
如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )| A. | 当∠β为定值时,∠CDE为定值 | B. | 当∠α为定值时,∠CDE为定值 | ||
| C. | 当∠γ为定值时,∠CDE为定值 | D. | ∠CDE的值与∠α,∠β,∠γ的值无关 |
分析 先利用AB=AC,可得∠B=∠C,同理可得∠ADE=∠AED,再利用外角性质可得∠ADC=∠B+∠α,∠AED=∠C+∠CDE,而∠ADC=∠ADE+∠CDE,等量代换可得∠C+∠CDE+∠CDE=∠B+∠α,化简得到∠CDE与∠α的关系:2∠CDE=∠α.
解答 解:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
又∵∠ADC=∠B+∠BAD=∠B+∠α,∠AED=∠C+∠CDE,
∴∠ADE+∠CDE=∠B+∠BAD=∠B+∠α,
即∠C+∠CDE+∠CDE=∠B+∠α,
∴2∠CDE=∠α,
∴∠CDE=$\frac{1}{2}$∠α.
即当∠α为定值时,∠CDE为定值,
故选B.
点评 本题考查了等腰三角形的性质、三角形外角的性质,正确识图并利用等腰三角形两底角相等的性质,三角形的一个外角等于和它不相邻的两个内角的和的性质理清各角的关系是解题的关键.


科目:初中数学 来源: 题型:选择题
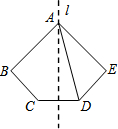 如图所示,五边形ABCDE关于过点A的直线l轴对称,若∠DAE=40°,∠ADE=60°,则∠B的度数为( )
如图所示,五边形ABCDE关于过点A的直线l轴对称,若∠DAE=40°,∠ADE=60°,则∠B的度数为( )| A. | 60° | B. | 40° | C. | 80° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
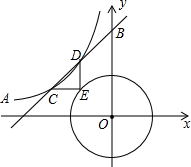 如图,直线y=x+3$\sqrt{2}$与反比例函数y=$\frac{k}{x}$的图象交于C、D两点,⊙O是以CD长为半径的圆,CE∥x轴,DE∥y轴,求k的值.
如图,直线y=x+3$\sqrt{2}$与反比例函数y=$\frac{k}{x}$的图象交于C、D两点,⊙O是以CD长为半径的圆,CE∥x轴,DE∥y轴,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
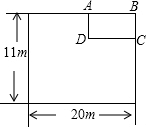 某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20m和11m的长方形大厅内修建一个长方形健身房ABCD.该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为a元/m2,比新建(含装修)墙壁的费用每平方米少50元.设健身房的高为3m,一面旧墙壁AB的长为xm,BC为(x-5)米,修建健身房墙壁的总投入为多少元?(用含a,x的代数式表示)
某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20m和11m的长方形大厅内修建一个长方形健身房ABCD.该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为a元/m2,比新建(含装修)墙壁的费用每平方米少50元.设健身房的高为3m,一面旧墙壁AB的长为xm,BC为(x-5)米,修建健身房墙壁的总投入为多少元?(用含a,x的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com