
分析 (1)找出十位数字为2的所有等可能的情况数,进而求出两人获胜的概率,比较即可得到结果;
(2)这个游戏对小伟和小欣是公平的.根据题意,由(1)的图表,分别计算两人谁获胜的可能性,比较可得答案.
解答 解:(1)列表得:
| 数字 | 1 | 2 | 3 | 4 |
| 1 | --- | 12 | 13 | 14 |
| 2 | 21 | --- | 23 | 24 |
| 3 | 31 | 32 | --- | 34 |
| 4 | 41 | 42 | 43 | --- |
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.游戏双方获胜的概率相同,游戏就公平,否则游戏不公平.用到的知识点为:概率=所求情况数与总情况数之比.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
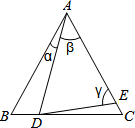 如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )
如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )| A. | 当∠β为定值时,∠CDE为定值 | B. | 当∠α为定值时,∠CDE为定值 | ||
| C. | 当∠γ为定值时,∠CDE为定值 | D. | ∠CDE的值与∠α,∠β,∠γ的值无关 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
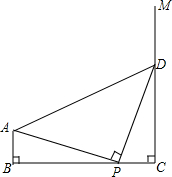 如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC(不与点B、C重合)上的点,过点P作DP⊥AP交射线CM于点D,连结AD.若BP=3,则△ABP的周长为4+$\sqrt{10}$.
如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC(不与点B、C重合)上的点,过点P作DP⊥AP交射线CM于点D,连结AD.若BP=3,则△ABP的周长为4+$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知多项式-2x2y3-4中,含字母项的系数记为a,多项式的次数记为b,常数项记为c,且a、b、c分别是点A、点B、点C在数轴上对应的数;
已知多项式-2x2y3-4中,含字母项的系数记为a,多项式的次数记为b,常数项记为c,且a、b、c分别是点A、点B、点C在数轴上对应的数;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
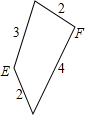 已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )| A. | $\frac{4}{3}$ | B. | $\frac{24}{5}$ | C. | $\frac{4}{3}$或$\frac{24}{5}$ | D. | $\frac{2}{3}$或$\frac{12}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com