
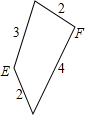
 已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )| A. | $\frac{4}{3}$ | B. | $\frac{24}{5}$ | C. | $\frac{4}{3}$或$\frac{24}{5}$ | D. | $\frac{2}{3}$或$\frac{12}{5}$ |
分析 分两种情况:点A为等腰三角形的顶点,点D为底边的中点与点D为等腰三角形的顶点,点A为底边的中点,利用等腰三角形的性质与相似三角形对应边的比相等的性质进行分析求解即可.
解答 解:如图1,当A为等腰三角形的顶点,点D为底边的中点时,设BD=DC=a,AB=AC=b,则BE=b-2,CF=b-4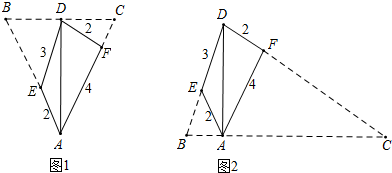 ,
,
∵AB=AC,
∴∠B=∠C,
又∵BD=DC,BE≠CF,DE≠DF,
∴点B与点C、点E与点D,点D与点F为对应点,即△BED∽△CDF,
∴BE:CD=ED:DF=BD:CF,即(b-2):a=3:2=a:(b-4),
解得a=$\frac{12}{5}$,
∴BC=2a=$\frac{24}{5}$;
如图2,当点D为等腰三角形的顶点,点A为底边的中点时,设BA=AC=a,BD=CD=b,则BE=b-3,CF=b-2,
∵BD=CD,
∴∠B=∠C,
∴点B与点C为对应点,
若点E与点F、点A与点C为对应点,
由△BEA∽△CFA,可得BE:CF=EA:FA=BA:CA,即(b-3):(b-2)=2:4=a:a,无解;
若点E与点A,点A与点F为对应点,
由△BEA∽△CAF,可得BE:CA=EA:AF=BA:CF,即(b-3):a=2:4=a:(b-2),解得a=$\frac{2}{3}$,b=$\frac{10}{3}$,
此时BA=$\frac{2}{3}$,BE=b-3=$\frac{1}{3}$,BE、BA、EA不能构成三角形,故此种情况不成立;
综上所述,这个等腰三角形底边长为$\frac{24}{5}$.
故选B.
点评 本题考查了等腰三角形的性质,相似三角形的判定与性质,难度适中,解答本题的关键是正确画出图形,并熟知相似三角形对应边的比相等的性质,同时注意分类讨论思想与方程思想的运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
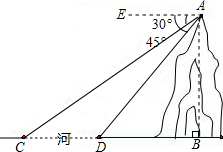 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为20米,求小山AB的高(答案可带根号)
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为20米,求小山AB的高(答案可带根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
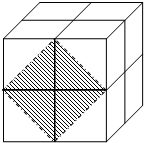 如图,这是由8个同样大小的立方体组成的魔方,体积为64cm3.
如图,这是由8个同样大小的立方体组成的魔方,体积为64cm3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向右平移2个单位 | B. | 向左平移2个单位 | C. | 向右平移4个单位 | D. | 向左平移4个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com