
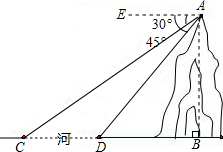
 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为20米,求小山AB的高(答案可带根号)
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为20米,求小山AB的高(答案可带根号) 分析 设小山AB的高为x米,在Rt△ABC中,∠ACB=30°,利用三角函数可以用x表示BC的长度,在Rt△ADB中,∠ADB=45°,可以得到BD=x,而BC-BD=CD,由此根据已知条件可以得到关于x的方程,解方程即可求解.
解答 解:设小山AB的高为x米.
∵在Rt△ABC中,∠ACB=30°,
∴BC=$\frac{AB}{tan30°}$=$\sqrt{3}$x,
∵在Rt△ADB中,∠ADB=45°,
∴BD=AB=x.
∵BC-BD=CD,
∴$\sqrt{3}$x-x=20,
解得x=10($\sqrt{3}$+1).
答:小山AB的高为10($\sqrt{3}$+1)米.
点评 此题主要考查了解直角三角形的应用-仰角俯角问题,解题的关键是正确理解俯角的定义,然后利用三角函数列出关于x的方程.


科目:初中数学 来源: 题型:解答题
 已知多项式-2x2y3-4中,含字母项的系数记为a,多项式的次数记为b,常数项记为c,且a、b、c分别是点A、点B、点C在数轴上对应的数;
已知多项式-2x2y3-4中,含字母项的系数记为a,多项式的次数记为b,常数项记为c,且a、b、c分别是点A、点B、点C在数轴上对应的数;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
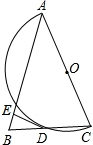 如图,在△ABC中,AB=AC,以AC为直径的半圆O与边BC相交于点D,DE⊥AB,垂足为E
如图,在△ABC中,AB=AC,以AC为直径的半圆O与边BC相交于点D,DE⊥AB,垂足为E查看答案和解析>>
科目:初中数学 来源: 题型:选择题
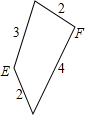 已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )| A. | $\frac{4}{3}$ | B. | $\frac{24}{5}$ | C. | $\frac{4}{3}$或$\frac{24}{5}$ | D. | $\frac{2}{3}$或$\frac{12}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)2=-2 | B. | $\sqrt{{{(-2)}^2}}$=4 | C. | (-$\sqrt{2}$)2=4 | D. | -($\sqrt{{2}^{2}}$)2=-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com