
分析 由5sin2α-7sinα+2.4=0,变形为$(sinα-\frac{3}{5})•(sinα-\frac{4}{5})=0$,从而得出$sinα=\frac{3}{5}$或$sinα=\frac{4}{5}$;过点P作PE⊥x轴于点E,则可得PE=6,0E=m,在Rt△POE中根据$sinα=\frac{3}{5}$或$sinα=\frac{4}{5}$,求出OP,继而根据勾股定理求得m的值,然后根据待定系数法即可求得反比例函数的解析式.
解答 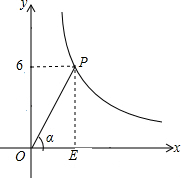 解:过点P作PE⊥x轴于点E,则可得PE=6,0E=m,
解:过点P作PE⊥x轴于点E,则可得PE=6,0E=m,
∵5sin2α-7sinα+2.4=0,
∴$(sinα-\frac{3}{5})•(sinα-\frac{4}{5})=0$,
∴$sinα=\frac{3}{5}$或$sinα=\frac{4}{5}$,
当$sinα=\frac{3}{5}$时,则sinα=$\frac{6}{OP}$=$\frac{3}{5}$
∴OP=10,
在RT△POE中,OE=$\sqrt{O{P}^{2}-P{E}^{2}}$=8,
∴m=8,此时,k=6×8=48,
∴$y=\frac{48}{x}$;
当$sinα=\frac{4}{5}$时,则sinα=$\frac{6}{OP}$=$\frac{4}{5}$
∴OP=$\frac{15}{2}$,由勾股定理得:m=$\frac{9}{2}$,此时,k=6×4.5=27,
∴$y=\frac{27}{x}$.
点评 本题考查了待定系数法求反比例函数的解析式、勾股定理及同角的三角函数关系,解答本题的关键是求出OP的长度.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
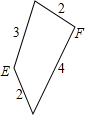 已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )| A. | $\frac{4}{3}$ | B. | $\frac{24}{5}$ | C. | $\frac{4}{3}$或$\frac{24}{5}$ | D. | $\frac{2}{3}$或$\frac{12}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
| A. | 15 | B. | 15.5 | C. | 16 | D. | 16.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8π | B. | 16π | C. | 4$\sqrt{3}$π | D. | 8$\sqrt{7}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)2=-2 | B. | $\sqrt{{{(-2)}^2}}$=4 | C. | (-$\sqrt{2}$)2=4 | D. | -($\sqrt{{2}^{2}}$)2=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{10}$-3.1 | B. | 3.1±$\sqrt{10}$ | C. | 3.1-$\sqrt{10}$ | D. | ±(3.1-$\sqrt{10}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com