在平面直角坐标系中.点A平移后能与原来的位置关于y轴轴对称.则应把点A( )A．向右平移2个单位B．向左平移2个单位C．向右平移4个单位D．向左平移4个单位题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

19．在平面直角坐标系中，点A（-2，3）平移后能与原来的位置关于y轴轴对称，则应把点A（　　）

A．

向右平移2个单位

B．

向左平移2个单位

C．

向右平移4个单位

D．

向左平移4个单位

分析关于y轴成轴对称的两个点的纵坐标相同，横坐标互为相反数，那么向右平移两个横坐标差的绝对值即可．

解答解：∵点A（-2，3）平移后能与原来的位置关于y轴轴对称，
∴平移后的坐标为（2，3），
∵横坐标增大，
∴点是向右平移得到，平移距离为|2-（-2）|=4．
故选C．

点评本题考查了平移中点的变化规律及点关于坐标轴对称的知识点，用到的知识点为：两点关于y轴对称，纵坐标相同，横坐标互为相反数；点的左右移动只改变点的横坐标．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

9．

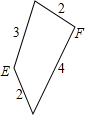已知有一块等腰三角形纸板，在它的两腰上各有一点E和F，把这两点分别与底边中点连结，并沿着这两条线段剪下两个三角形，所得的这两个三角形相似，剩余部分（四边形）的四条边的长度如图所示，那么原等腰三角形的底边长为（　　）

A．

$\frac{4}{3}$

B．

$\frac{24}{5}$

C．

$\frac{4}{3}$或$\frac{24}{5}$

D．

$\frac{2}{3}$或$\frac{12}{5}$

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

10．下列计算正确的是（　　）

A．

（-1）²=-2

B．

$\sqrt{{{（-2）}^2}}$=4

C．

（-$\sqrt{2}$）²=4

D．

-（$\sqrt{{2}^{2}}$）²=-4

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

7．若-x⁴y⁶与3x^m-1y³ⁿ是同类项，则mⁿ=25．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

14．下列结论正确的是（　　）

A．

$-\sqrt{（-6）^{2}}=-6$

B．

$（-\sqrt{3}）^{2}=9$

C．

$\sqrt{（{-16）}^{2}}=±16$

D．

$-（-\sqrt{\frac{16}{25}}）^{2}=\frac{16}{25}$

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．阅读材料，解答问题．
例：若代数式$\sqrt{{{（2-a）}^2}}+\sqrt{{{（a-4）}^2}}$的值是常数2，则a的取值范围2≤a≤4．
分析：原式=|a-2|+|a-4|，而|a|表示数a在数轴上的点到原点的距离，|a-2|表示数a在数轴上的点到数2的点的距离，所以我们可以借助数轴进行分析．

解：原式=|a-2|+|a-4|
在数轴上看，讨论a在数2表示的点左边；在数2表示的点和数4表示的点之间还是在数4表示的点右边，分析可得a的范围应是2≤a≤4．
（1）此例题的解答过程了用了哪些数学思想？请列举．
（2）化简$\sqrt{{{（3-a）}^2}}+\sqrt{{{（a-7）}^2}}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．（1）如图1，已知OC是∠AOB内部的一条射线，∠AOC=30°，OE是∠COB的平分线．当∠COE=40°时，求∠AOB的度数；
（2）如图2，已知射线Ox与射线Oy互相垂直，B，A分别为Ox、Oy上一动点，∠ABx、∠BAy的平分线交于C．问：B、A在Ox、Oy上运动过程中，∠C的度数是否改变？若不改变，求出其值；若改变，说明理由．
（3）如图3，E和D分别在△ABC的边BA和CA的延长线上，CF、EF分别平分∠ACB和∠AED，若∠B=70°，∠D=40°，求∠F的大小．