
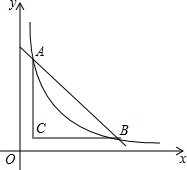
 如图,将一块直角三角形纸板的直角顶点放在C(1,$\frac{1}{2}$),处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+$\frac{9}{2}$与双曲线y=$\frac{m}{x}$(m>0)的交点
如图,将一块直角三角形纸板的直角顶点放在C(1,$\frac{1}{2}$),处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+$\frac{9}{2}$与双曲线y=$\frac{m}{x}$(m>0)的交点分析 (1)由AC平行于y轴,BC平行于x轴,根据C坐标,得出A的横坐标与B的纵坐标,分别代入直线与双曲线解析式,求出k与m的值即可;
(2)由(1)确定出A与B坐标,如图所示,分三种情况考虑,利用平行四边形的性质分别求出D坐标即可.
解答 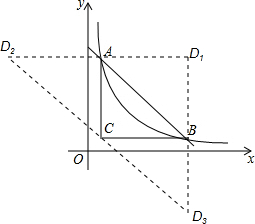 解:(1)∵AC∥y轴,BC∥x轴,且C(1,$\frac{1}{2}$),
解:(1)∵AC∥y轴,BC∥x轴,且C(1,$\frac{1}{2}$),
∴A横坐标为1,B纵坐标为$\frac{1}{2}$,
把x=1代入直线与双曲线得:k+$\frac{9}{2}$=m①,
把y=$\frac{1}{2}$代入直线与双曲线得:-$\frac{4}{k}$=2m②,
联立①②,解得:m=4,k=-$\frac{1}{2}$或m=$\frac{1}{2}$,k=-4(不合题意,舍去),
则m=4,k=-$\frac{1}{2}$;
(2)由(1)得:A(1,4),B(8,$\frac{1}{2}$),
如图所示,分三种情况考虑:
当四边形ACBD1为平行四边形时,由∠ACB=90°,得到四边形为矩形,此时D1(8,4);
当四边形ABCD2为平行四边形时,AD2=BC=7,此时D2(-6,4);
当四边形ABD3C为平行四边形时,BD3=AC=3$\frac{1}{2}$,此时D3(8,-3),
综上,D的坐标为(8,4)或(-6,4)或(8,-3).
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法确定函数解析式,坐标与图形性质,平行四边形的性质,熟练掌握性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
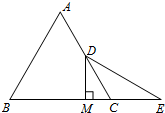 如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,
如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了解10000个灯泡的使用寿命,选择普查 | |
| B. | 为了解某鱼塘中鱼的质量,选择普查 | |
| C. | 为了解某班级学生的视力情况,选择普查 | |
| D. | 为了解一批袋装食品是否有防腐剂,选择普查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中复习检测数学试卷(一)(解析版) 题型:单选题
下列计算错误的是( )
A. (-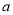 )2·(-
)2·(-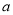 )=-
)=-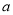 3 B.
3 B. 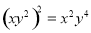 C.
C. 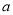 7÷
7÷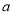 7=1 D. 2
7=1 D. 2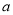 4·3
4·3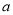 2=6
2=6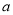 8
8
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
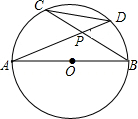 已知:如图,AB是⊙O的直径,弦AD、BC相交于P点,那么$\frac{DC}{AB}$的值为( )
已知:如图,AB是⊙O的直径,弦AD、BC相交于P点,那么$\frac{DC}{AB}$的值为( )| A. | sin∠APC | B. | cos∠APC | C. | tan∠APC | D. | $\frac{1}{tan∠APC}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com