
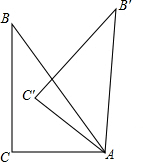
 如图,在△ABC中,∠C=90°,∠BAC=60°,AC=2,将△ABC绕点A顺时针旋转α(0°<α<180°),记旋转中△ABC为△A′B′C′,在旋转过程中B′C′所在的直线与线段BC(不含B点)交于点P,与线段AB(不含B点)交于点Q,当BP=BQ时,PQ=2$\sqrt{6}$+4$\sqrt{3}$-2$\sqrt{2}$-8.
如图,在△ABC中,∠C=90°,∠BAC=60°,AC=2,将△ABC绕点A顺时针旋转α(0°<α<180°),记旋转中△ABC为△A′B′C′,在旋转过程中B′C′所在的直线与线段BC(不含B点)交于点P,与线段AB(不含B点)交于点Q,当BP=BQ时,PQ=2$\sqrt{6}$+4$\sqrt{3}$-2$\sqrt{2}$-8. 分析 如图,利用含30度的直角三角形三边的关系得AB=2AC=4,BC=$\sqrt{3}$AC=2$\sqrt{3}$,再根据旋转的性质得AB=AB′=4,BC=B′C′=2$\sqrt{3}$,∠B=∠B′=30°,∠B′AC=∠BAC=60°,由于BP=BQ,则根据等腰三角形的性质和三角形内角和可计算出∠BPQ=∠BQP=75°,∠AQC′=∠BQP=∠B′AQ=75°,所以B′Q=B′A=4,于是可得到C′Q=B′Q-B′C′=4-2$\sqrt{3}$,在Rt△AQC′中,根据勾股定理计算出AQ=2($\sqrt{6}$-$\sqrt{2}$),则BQ=AB-AQ=4-2($\sqrt{6}$-$\sqrt{2}$),然后证明△BPQ∽△B′AQ,则利用相似比可计算出PQ.
解答 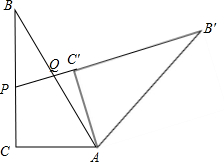 解:如图,
解:如图,
∵∠C=90°,∠BAC=60°,
∴AB=2AC=4,BC=$\sqrt{3}$AC=2$\sqrt{3}$,
∵△ABC绕点A顺时针旋转α(0°<α<180°),记旋转中△ABC为△A′B′C′,
∴AB=AB′=4,BC=B′C′=2$\sqrt{3}$,∠B=∠B′=30°,∠B′AC=∠BAC=60°,
∵BP=BQ,
∴∠BPQ=∠BQP=$\frac{1}{2}$(180°-30°)=75°,
∴∠AQC′=∠BQP=75°,
∴∠B′AQ=180°-75°-30°=75°,
∴B′Q=B′A=4,
∴C′Q=B′Q-B′C′=4-2$\sqrt{3}$,
在Rt△AQC′中,AQ=$\sqrt{QC{′}^{2}+A{C}^{′2}}$=$\sqrt{(4-2\sqrt{3})^{2}+{2}^{2}}$=2($\sqrt{6}$-$\sqrt{2}$),
∴BQ=AB-AQ=4-2($\sqrt{6}$-$\sqrt{2}$),
∵△BPQ∽△B′AQ,
∴$\frac{PQ}{AQ}$=$\frac{BQ}{B′A}$,即$\frac{PQ}{2(\sqrt{6}-\sqrt{2})}$=$\frac{4-2(\sqrt{6}-\sqrt{2})}{4}$,
∴PQ=2$\sqrt{6}$+4$\sqrt{3}$-2$\sqrt{2}$-8.
故答案为2$\sqrt{6}$+4$\sqrt{3}$-2$\sqrt{2}$-8.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了解直角三角形和相似三角形的判定与性质.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:解答题
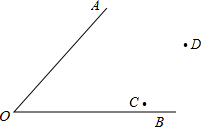 OA、OB为两条笔直的公路,C、D为两个工厂,现欲在附近建一个货运站,使得它到两条公路距离相等,到两家工厂距离也相等.请作出符合条件的货运站P.不写作法,保留作图痕迹.
OA、OB为两条笔直的公路,C、D为两个工厂,现欲在附近建一个货运站,使得它到两条公路距离相等,到两家工厂距离也相等.请作出符合条件的货运站P.不写作法,保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
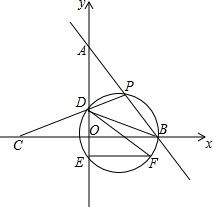 如图,在平面直角坐标系中,O为坐标原点,直线y=-$\frac{4}{3}$x+4与x轴交于点B,与y轴交于点A,点C在x轴的负半轴上,并且OC=OB,一动点P在射线AB上运动,连结CP交y轴于点D,连结BD.过B,P,D三点作圆,交y轴与点E,过点E作EF∥x轴,交圆于点F,连结BF,DF.
如图,在平面直角坐标系中,O为坐标原点,直线y=-$\frac{4}{3}$x+4与x轴交于点B,与y轴交于点A,点C在x轴的负半轴上,并且OC=OB,一动点P在射线AB上运动,连结CP交y轴于点D,连结BD.过B,P,D三点作圆,交y轴与点E,过点E作EF∥x轴,交圆于点F,连结BF,DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
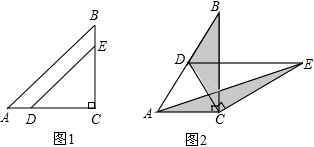
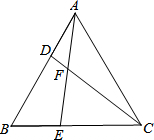 已知△ABC,其中AB=BC=AC,∠BAC=∠B=∠ACB=60°,点D、E分别在AB、BC上且AD=BE,线段AE、CD相交于点F.
已知△ABC,其中AB=BC=AC,∠BAC=∠B=∠ACB=60°,点D、E分别在AB、BC上且AD=BE,线段AE、CD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 6 | 1 | 2x-4 |
| y-x | 3y-x | 7 |
| 4 | 5 | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com