
【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BD=CE

(1)问△ABC为等腰三角形吗?为什么?
(2)问点O在∠A的平分线上吗?为什么?
【答案】(1)是,理由参见解析;(2)在,理由参见解析.
【解析】
(1)利用HL证明Rt△BCE≌Rt△DCB,由全等得到∠ABC=∠ACB,从而得到AB=AC,可知△ABC为等腰三角形;
(2)由Rt△BCE≌Rt△DCB,得到BE=CD,再利用AAS证明△EOB≌△DOC,从而得到OE=OD,又因为BD、CE分别是AC、AB上的高,所以OE⊥AB,OD⊥AC,根据角平分线的判定定理可知点O在∠A的平分线上.
(1)![]() BD、CE分别是AC、AB上的高,
BD、CE分别是AC、AB上的高,
![]() ∠CEB=∠BDC=90°
∠CEB=∠BDC=90°
又![]() BD=CE,BC=CB,
BD=CE,BC=CB,
![]() Rt△BCE≌Rt△DCB(HL),
Rt△BCE≌Rt△DCB(HL),
![]() ∠ABC=∠ACB(全等三角形对应角相等)
∠ABC=∠ACB(全等三角形对应角相等)
![]() AB=AC(等角对等边),
AB=AC(等角对等边),
![]() △ABC为等腰三角形;
△ABC为等腰三角形;
(2)![]() Rt△BCE≌Rt△DCB,
Rt△BCE≌Rt△DCB,
![]() BE=CD(全等三角形对应边相等),
BE=CD(全等三角形对应边相等),
在△EOB和△DOC中,∠EOB=∠DOC,∠OEB=∠ODC=90°,
![]() △EOB≌△DOC(AAS),
△EOB≌△DOC(AAS),
![]() OE=OD,
OE=OD,
![]() OE⊥AB,OD⊥AC,根据角平分线的判定定理(到角的两边距离相等的点在这个角的平分线上)可知点O在∠A的平分线上.
OE⊥AB,OD⊥AC,根据角平分线的判定定理(到角的两边距离相等的点在这个角的平分线上)可知点O在∠A的平分线上.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中.
(1)写出点A,点B的坐标A( , ),B( , );
(2)S△ABC= ;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1的位置,并写出点A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB、AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A、E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF=![]() ,④S△CGE:S△CAB=1:4.其中正确的是( )
,④S△CGE:S△CAB=1:4.其中正确的是( )
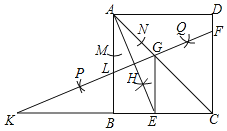
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个各数位上的数字均不为![]() 的三位自然数
的三位自然数![]() ,将它各个数位上的数字平方后再取其个位,得到三个新的数字;再将这三个新数字重新组合成三位数
,将它各个数位上的数字平方后再取其个位,得到三个新的数字;再将这三个新数字重新组合成三位数![]() ,当
,当![]() 的值最小时,称此时的
的值最小时,称此时的![]() 为自然数
为自然数![]() 的“理想数”,并规定:
的“理想数”,并规定:![]() ,例如
,例如![]() ,各数字平方后取个位分别为
,各数字平方后取个位分别为![]() ,
,![]() ,
,![]() ,再重新组合为
,再重新组合为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,因为
,因为![]() 最小,所以
最小,所以![]() 是原三位数
是原三位数![]() 的理想数,此时
的理想数,此时![]()
(1)求:![]() .
.
(2)若有三位自然数![]() ,满足有两个数位上的数字相同且不等于
,满足有两个数位上的数字相同且不等于![]() ,另一个数位上的数字为
,另一个数位上的数字为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师准备了四张背面看上去无差别的卡片A,B,C,D,每张卡片的正面标有字母a,b,c表示三条线段(如图),把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.

(1)用树状图或者列表表示所有可能出现的结果;
(2)求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查![]() 每个被调查的学生必须选择而且只能选择其中一门
每个被调查的学生必须选择而且只能选择其中一门![]() 对调查结果进行整理,绘制成如下两幅不完整的统计图
对调查结果进行整理,绘制成如下两幅不完整的统计图![]() 请结合图中所给信息解答下列问题:
请结合图中所给信息解答下列问题:


![]() 本次调查的学生共有______人,在扇形统计图中,m的值是______.
本次调查的学生共有______人,在扇形统计图中,m的值是______.
![]() 分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
![]() 该校共有学生2000人,估计该校约有多少人选修乐器课程?
该校共有学生2000人,估计该校约有多少人选修乐器课程?
查看答案和解析>>
科目:初中数学 来源: 题型:
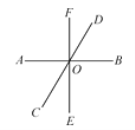
【题目】如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,![]() ,求∠DOF和∠FOC的度数.
,求∠DOF和∠FOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题的大意是:有一块三角形沙田,三条边长分别为5里;12里;13里,问这块沙田面积有多大?题中的1里=0.5千米,则该沙田的面积为( )
A.3平方千米B.7.5平方千米C.15平方千米D.30平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com