
【题目】如图,一个均匀的转盘被平均分成8等份,分别标有2,4,6,8,10,12,14,16这8个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.小亮与小颖参与游戏:小亮转动转盘,小颖猜数,若所猜数字与转出的数字相符,则小颖获胜,否则小亮获胜.
(1)若小颖猜是“3的倍数”,则她获胜的概率为 ;
(2)若小颖猜是“奇数”,则她获胜的概率是 ;
(3)请你用这个转盘设计一个游戏,使得对小亮与小颖均是公平的;
(4)小颖发现,当她猜的数字是“10”时,她连续获胜了10次.请问有可能吗?为什么?

【答案】(1)![]() ;(2)0;(3)设计为:小颖猜是“4的倍数”小颖获胜,否则小亮获胜;(4)有可能,见解析.
;(2)0;(3)设计为:小颖猜是“4的倍数”小颖获胜,否则小亮获胜;(4)有可能,见解析.
【解析】
(1) 8个数中有3个数为3的倍数,则可根据概率公式计算小颖获胜的概率;
(2) 由于8个数中没有奇数,则可根据不可能事件得概率求解;
(3) 利用8个数有4个为4的倍数设计游戏规则;
(4) 利用转盘可能连续10次指向的数字为10可说明她可能连续获胜10次.
(1) 若小颖猜是“3的倍数”,则她获胜的概率=![]() ,
,
故答案为:![]() ;
;
(2) 若小颖猜是“奇数”,则她获胜的概率=0,
故答案为:0;
(3) 设计为:小颖猜是“4的倍数”小颖获胜,否则小亮获胜;
(4) 有可能.因为她猜的数字是“10”时,转动转盘,可能连续10次指向的数字为10,则她连续获胜了10次.


科目:初中数学 来源: 题型:
【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=![]() OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人连续6年调查某地养鱼业的情况,提供了两方面的信息图(如图).甲调查表明:每个鱼池平均产量从第1年的1万条上升到第6年的2万条;乙调查表明:该地养鱼池的个数由第1年的30个减少到第6年的10个. 现给出下列四个判断:①该地第3年养鱼池产鱼数量为1.4万条;②该地第2年养鱼池产鱼的数量低于第3年养鱼池产鱼的数量;③该地这6年养鱼池产鱼的数量逐年减少;④这6年中,第6年该地养鱼池产鱼的数量最少.根据甲、乙两人提供的信息,可知其中正确的判断有( ).
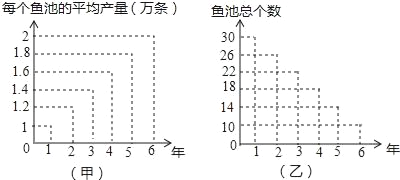
A. ①④ B. ④ C. ②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
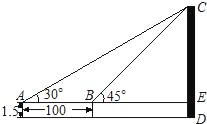
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取![]() =1.732,结果精确到1m)
=1.732,结果精确到1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃ | … | ﹣5 | ﹣3 | 2 | … |
植物高度增长量h/mm | … | 34 | 46 | 41 | … |
科学家推测出h(mm)与t之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为( )
A. ﹣2℃ B. ﹣1℃ C. 0℃ D. 1℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:


根据以上信息,整理分析数据如下:
平均月收入/千元 | 中位数/千元 | 众数/千元 | 方差/千元2 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com