
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,点
,点![]() 是
是![]() 上的一点,且
上的一点,且![]() ,
,![]() .
.
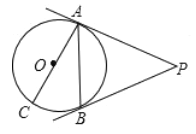
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为2,求弦
的半径为2,求弦![]() 及
及![]() ,
,![]() 的长.
的长.
【答案】(1)见解析;(2)PA=PB=AB=2![]() .
.
【解析】
(1)连接OB,证PB⊥OB.根据四边形的内角和为360°,结合已知条件可得∠OBP=90°得证.
(2)连接OP,根据切线长定理得直角三角形,运用三角函数求解.
(1)证明:连接OB.
∵OA=OB,
∴∠OBA=∠BAC=30°.
∴∠AOB=180°-30°-30°=120°.
∵PA切⊙O于点A,
∴OA⊥PA,
∴∠OAP=90°.
∵四边形的内角和为360°,
∴∠OBP=360°-90°-60°-120°=90°.
∴OB⊥PB.
又∵点B是⊙O上的一点,
∴PB是⊙O的切线.
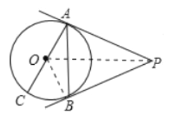
(2)连接OP;
∵PA、PB是⊙O的切线,
∴PA=PB,∠OPA=∠OPB=![]() ∠APB=30°.
∠APB=30°.
在Rt△OAP中,∠OAP=90°,∠OPA=30°,
∴OP=2OA=2×2=4,
∴PA=![]() =
=![]() =2
=2![]() .
.
∵PA=PB,∠APB=60°,
∴PA=PB=AB=2![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
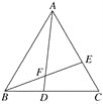
【题目】如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证:
(1)△ABD≌△BCE;
(2)△AEF∽△ABE.
查看答案和解析>>
科目:初中数学 来源: 题型:
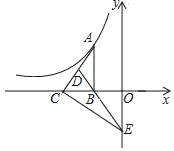
【题目】如图,Rt△ABC的直角边BC在x轴负半轴上,斜边AC上的中线BD的反向延长线交y轴负半轴于点E,反比例函数y=﹣![]() (x<0)的图象过点A,则△BEC的面积是_____.
(x<0)的图象过点A,则△BEC的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一直角三角形放置在如图所示的平面直角坐标系中,直角顶点C刚好落在反比例函数y=![]() 的图象的一支上,两直角边分别交y、x轴于A、B两点.当CA=CB时,四边形CAOB的面积为( )
的图象的一支上,两直角边分别交y、x轴于A、B两点.当CA=CB时,四边形CAOB的面积为( )
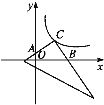
A. 4 B. 8 C. 2![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
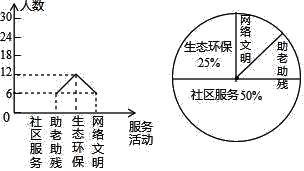
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
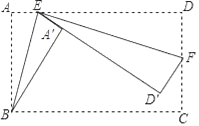
【题目】如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2﹣6x+c的图象过A(﹣1,y1),B(2,y2),C(3,y3),则y1、y2、y3的大小关系是( )
A. y1>y2>y3 B. y1>y3>y2 C. y2>y1>y3 D. y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个均匀的转盘被平均分成8等份,分别标有2,4,6,8,10,12,14,16这8个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.小亮与小颖参与游戏:小亮转动转盘,小颖猜数,若所猜数字与转出的数字相符,则小颖获胜,否则小亮获胜.
(1)若小颖猜是“3的倍数”,则她获胜的概率为 ;
(2)若小颖猜是“奇数”,则她获胜的概率是 ;
(3)请你用这个转盘设计一个游戏,使得对小亮与小颖均是公平的;
(4)小颖发现,当她猜的数字是“10”时,她连续获胜了10次.请问有可能吗?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com