
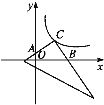
【题目】一直角三角形放置在如图所示的平面直角坐标系中,直角顶点C刚好落在反比例函数y=![]() 的图象的一支上,两直角边分别交y、x轴于A、B两点.当CA=CB时,四边形CAOB的面积为( )
的图象的一支上,两直角边分别交y、x轴于A、B两点.当CA=CB时,四边形CAOB的面积为( )
A. 4 B. 8 C. 2![]() D.
D. ![]()
【答案】B
【解析】
作CE垂直x轴于点E,AF⊥CE于点F,CM垂直于y轴于点M,AC交x轴于点N,求出△AFC≌△CEB得到AF=CE=2![]() ,再利用四边形CAOB的面积=正方形MOEC的面积即可得答案.
,再利用四边形CAOB的面积=正方形MOEC的面积即可得答案.
作CE垂直x轴于点E,AF⊥CE于点F,CM垂直于y轴于点M,AC交x轴于点N,
∵∠NOA=∠NCB=90°,∠ANO=∠BNC,
∴△ANO∽△CNB,
∴∠NAO=∠NBC,
又∵AO∥CE,
∴∠NAO=∠ACF,
∴∠ACF=∠NBC,即∠ACF=∠EBC
∵∠AFC=∠CEB=90°,AC=CB,∠ACF=∠EBC,
∴△AFC≌△CEB(AAS)
∵四边形MAFC是矩形,
∴△AFC≌△MAC,
∴△CEB≌△MAC,
∴S△CEB=S△MAC,
∴AF=CE,
∵AF=CM
∴CM=BE
∴C点的横坐标与纵坐标相等,
∵点C在反比例函数y=![]() 的图像上,
的图像上,
∴AF×CE=8,
∴AF=CE=2![]()
∵S四边形CAOB=S四边形CAOE+S△CEB= S四边形CAOE+S△MAC=S正方形MOEC=(2![]() )2=8.
)2=8.

故选B.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程m x2-(m+2)x+2=0(m≠0).
(1)求证:无论m为何值时,这个方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
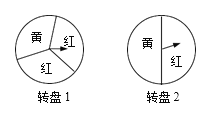
【题目】小玲为毕业联欢会设计了一个“配橙色”的游戏,使用的是如图所示两个可以自由转动的转盘,每个转盘被分成面积相等的若干个扇形,不同扇形分别填涂颜色,分界线可忽略,游戏者同时转动两个转盘,两个转盘停止转动时,若有一个转盘的指针指向红色,另一个转盘的指针指向黄色,则“配橙色”游戏成功,游戏者获胜.求游戏者获胜的概率.(用列表法或画树状图说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小彤根据学习函数的经验,对函数y=
的图象与性质.小彤根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小彤探究的过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
则m的值为 ;
(3)如图所示,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
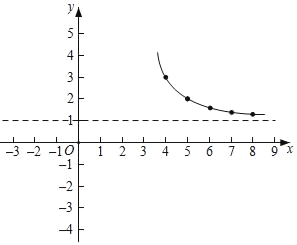
(4)观察图象,写出该函数的一条性质 ;
(5)若函数y=![]() 的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为 ;
的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
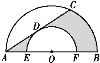
【题目】如图,AB是半圆O的直径,以O为圆心,OE长为半径的小半圆交AB于E,F两点,弦AC是小半圆的切线,D为切点,已知AO=4,EO=2,那么阴影部分的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在铅直高度为200 m的小山上建有一座电视转播塔,某数学兴趣小组为测量电视转播塔的高度,在山脚的点C处测得山顶B的仰角为30°(即∠BCD=300),测得塔顶A的仰角为45°(即∠ACD=45°),请根据以上数据求塔高AB(精确到1 m)(备用数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
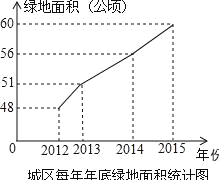
【题目】美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
(1)根据图中所提供的信息回答下列问题:2015年底的绿地面积为 公顷,比2014年底增加了 公顷;在2013年,2014年,2015年这三年中,绿地面积增加最多的是 年;
(2)为满足城市发展的需要,计划到2017年底使城区绿地面积达到72.6公顷,试求今明两年绿地面积的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com