
����Ŀ��Ϊ����������ס��Ѱ�����������������־Ը�����������������ˡ��������ҡ���־Ը��������Ϸ���ij��ѧ������ĩʱ�俪չ�ˡ��������С�����������̬�����������������ĸ�־Ը������ÿ��ֻ�μ�һ����������꼶ij��ȫ��ͬѧ���μ���־Ը���Ϊ�˽�־Ը�����������ռ��������ݺ������²�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺
��1���������ͳ��ͼ����������
��2��������ͳ��ͼ�У������������ֶ�Ӧ��Բ�ĽǵĶ�����
��3��С����С���μ���־Ը������������״ͼ���б���������Dzμ�ͬһ�����ĸ��ʣ�
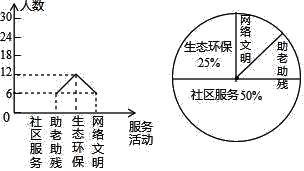
���𰸡���1���ð�ȫ������48�����������������Ϊ24������ȫ����ͳ����ͼ��ʾ����������2�������������ֶ�Ӧ��Բ�ĽǵĶ���Ϊ45�㣻��3�����Dzμ�ͬһ�����ĸ���Ϊ![]() ��
��
��������
��1�����ݲμ���̬�����������Լ��ٷֱ�������������������������������������ٷֱ���������������ɽ�����⣻
��2������Բ�Ľ�=360����ٷֱȣ����㼴�ɣ�
��3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ�������Dzμ�ͬһ����������������ø��ʹ�ʽ��⼴����ô𰸣�
��1���ð�ȫ��������12��25%=48�ˣ�
�������������Ϊ48��50%=24��
��ȫ����ͳ����ͼ��ʾ��
��2�������������ֶ�Ӧ��Բ�ĽǵĶ���Ϊ360����![]() =45�㣻
=45�㣻
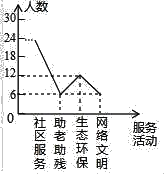
��3���ֱ���A��B��C��D��ʾ�����������������С���̬�����������������ĸ�������
����״ͼ�ã�
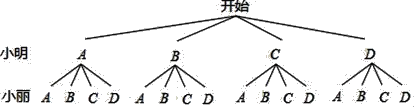
������16�ֵȿ��ܵĽ�������Dzμ�ͬһ��������4�������
�����Dzμ�ͬһ�����ĸ���Ϊ![]() ��
��


 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��a��0����ͼ��x����A��B���㣬��y���ڵ�D����B������Ϊ��3��0��������C������Ϊ��1��4����
��a��0����ͼ��x����A��B���㣬��y���ڵ�D����B������Ϊ��3��0��������C������Ϊ��1��4����
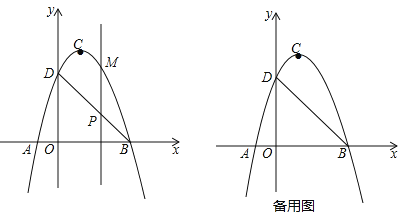
��1������κ����Ľ���ʽ��ֱ��BD�Ľ���ʽ��
��2����P��ֱ��BD�ϵ�һ�����㣬����P��x��Ĵ��ߣ����������ڵ�M������P�ڵ�һ����ʱ�����߶�PM���ȵ����ֵ��
��3�������������Ƿ��������B��D�ĵ�Q��ʹ��BDQ��BD���ϵĸ�Ϊ![]() �������������Q�����ꣻ����������˵�����ɣ�
�������������Q�����ꣻ����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У�AB=4��BC=5��AC�ij���һԪ���η���x2��15x+54=0��һ������
��1����AC�ij���
��2����AC����һ��D������BD��ʹ��ABD�ס�ACB��
��3����ACΪһ����һ��������ACM�����sin��AMC��ֵ���������������Լ���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=��x2+bx+c��c��0����ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����OB=OC=3������ΪM��
��1������κ����Ľ���ʽ��
��2����PΪ�߶�BM�ϵ�һ�����㣬����P��x��Ĵ���PQ������ΪQ����OQ=m���ı���ACPQ�����ΪS����S����m�ĺ�������ʽ����д��m��ȡֵ��Χ��
��3��̽�����߶�BM���Ƿ���ڵ�N��ʹ��NMCΪ���������Σ�������ڣ������N�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڰ뾶Ϊ2cm��Բ�Ľ�Ϊ90�������OAB�У��ֱ���OA��OBΪֱ������Բ����ͼ����Ӱ���ֵ����Ϊ_____��
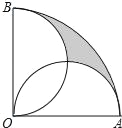
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=10��AC=8��BC=6���Ա�AB���е�OΪԲ�ģ�����Բ��AC���У���P��Q�ֱ��DZ�BC�Ͱ�Բ�ϵĶ��㣬����PQ����PQ������Сֵ��_______.
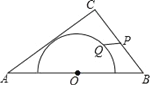
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ADΪ��BAC��ƽ���ߣ���������������֤����ABD�ա�ACD���ǣ�������

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���C��90����AC��BC��D��E�ֱ���AC��BC�ϣ�����DBC��2��BAE��AB��4![]() ��CD��
��CD��![]() ����CE�ij�Ϊ_____��
����CE�ij�Ϊ_____��
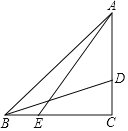
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֽƬABCD��AB=9��BC=6���ھ��α�����һ��P����DP=3��������ֽƬ�۵���ʹ��B���P�غϣ��ۺ�����ֱ�߽����������ڵ�E��F����EF��Ϊ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com