
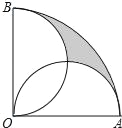
【题目】如图,在半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为_____.
【答案】![]() ﹣1.
﹣1.
【解析】
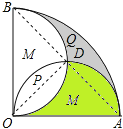
试题假设出扇形半径,再表示出半圆面积,以及扇形面积,进而即可表示出两部分P,Q面积相等.连接AB,OD,根据两半圆的直径相等可知∠AOD=∠BOD=45°,故可得出绿色部分的面积=S△AOD,利用阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色,故可得出结论.
解:∵扇形OAB的圆心角为90°,扇形半径为2,
∴扇形面积为:![]() =π(cm2),
=π(cm2),
半圆面积为:![]() ×π×12=
×π×12=![]() (cm2),
(cm2),
∴SQ+SM =SM+SP=![]() (cm2),
(cm2),
∴SQ=SP,
连接AB,OD,
∵两半圆的直径相等,
∴∠AOD=∠BOD=45°,
∴S绿色=S△AOD=![]() ×2×1=1(cm2),
×2×1=1(cm2),
∴阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色=π﹣![]() ﹣1=
﹣1=![]() ﹣1(cm2).
﹣1(cm2).
故答案为:![]() ﹣1.
﹣1.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李以每千克0.8元的价格从批发市场购进若干千克的西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完,销售金额与西瓜的千克数之间的关系如图所示,那么小李赚了( )
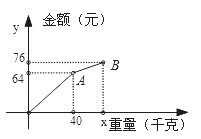
A. 32元B. 36元C. 38元D. 44元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() +
+![]() +2与x轴相交于A,B两点,(点A在B点左侧)与y轴交于点C.
+2与x轴相交于A,B两点,(点A在B点左侧)与y轴交于点C.
(1)求A,B两点坐标.
(2)连结AC,若点P在第一象限的抛物线上,P的横坐标为t,四边形ABPC的面积为S.试用含t的式子表示S,并求t为何值时,S最大.

(3)在(2)的基础上,在整条抛物线上和对称轴上是否分别存在点G和点H,使以A,G,H,P四点构成的四边形为平行四边形?若存在,请直接写出G,H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年春北方严重干旱,某社区人畜饮水紧张,每天需从社区外调运饮用水120吨,有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨,从两水厂运水到社区供水点的路程和运费如下表:
到社区供水点的路程(千米) | 运费(元/吨·千米) | |
甲厂 | 20 | 12 |
乙厂 | 14 | 15 |
【1】若某天调运水的总运费为26700元,则从甲、乙两水厂各调运多少吨饮用水?
【2】设从甲厂调运饮用水![]() 吨,总运费为W元,试写出W关于与
吨,总运费为W元,试写出W关于与![]() 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以直线x=![]() 对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y轴交于C(0,5),直线l与y轴交于点D.
对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y轴交于C(0,5),直线l与y轴交于点D.
(1)求抛物线的函数表达式;
(2)设直线l与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若![]() ,且△BCG与△BCD面积相等,求点G的坐标;
,且△BCG与△BCD面积相等,求点G的坐标;
(3)若在x轴上有且仅有一点P,使∠APB=90°,求k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
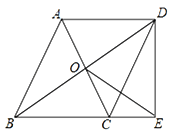
【题目】如图,□ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:△BDE是直角三角形;
(2)如果OE⊥CD,试判断△BDE与△DCE是否相似,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com