
����Ŀ����ͼ��������y=��![]() +
+![]() +2��x���ཻ��A��B���㣬����A��B����ࣩ��y�ύ�ڵ�C��
+2��x���ཻ��A��B���㣬����A��B����ࣩ��y�ύ�ڵ�C��
��1����A��B�������꣮
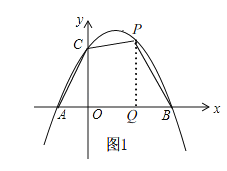
��2������AC������P�ڵ�һ�����������ϣ�P�ĺ�����Ϊt���ı���ABPC�����ΪS�����ú�t��ʽ�ӱ�ʾS������tΪ��ֵʱ��S���

��3���ڣ�2���Ļ����ϣ��������������ϺͶԳ������Ƿ�ֱ���ڵ�G�͵�H��ʹ��A��G��H��P�ĵ㹹�ɵ��ı���Ϊƽ���ı��Σ������ڣ���ֱ��д��G��H�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��A����![]() ��0����B��2
��0����B��2![]() ��0������2����t=
��0������2����t=![]() ʱ��S���=4
ʱ��S���=4![]() ����3�����������ĵ�P������ΪG����
����3�����������ĵ�P������ΪG����![]() ����
����![]() ����H��
����H��![]() ����
����![]() ����G��
����G��![]() ����
����![]() ����H��
����H��![]() ����
����![]() ����G����
����G����![]() ��
��![]() ����H��
����H��![]() ��
��![]() ����
����
��������
��1����y=0����![]() ���
���![]() ��
��![]() ���������A��B�������꣮
���������A��B�������꣮
��2����P��PQ��x����Q��P�ĺ�����Ϊt����P��t��p������![]() ��
��![]() ����S=S��AOC+S����OCPQ+S��PQB�г�S��t�ĺ�����ϵʽ�����ݶ��κ���������tΪ��ֵʱ��S���
����S=S��AOC+S����OCPQ+S��PQB�г�S��t�ĺ�����ϵʽ�����ݶ��κ���������tΪ��ֵʱ��S���
��3�������ߵĶԳ���Ϊ��![]() �ֱ�ʾ��ͼ������ƽ���ı��ε����ʼ������G��H������.
�ֱ�ʾ��ͼ������ƽ���ı��ε����ʼ������G��H������.
�⣺��1�������������![]() ��
��
��y=0����![]()
���![]() ��
��![]()
��![]()
��2�������������![]()
��x=0��
��y=2��
��C��0��2����
��ͼ1����P��PQ��x����Q��
��P�ĺ�����Ϊt��
����P��t��p����
��![]() ��
��![]()
��S=S��AOC+S����OCPQ+S��PQB
![]() ��
��
![]()
![]()
![]()
![]()
![]()
�൱![]() ʱ��S���
ʱ��S���![]()
��3�����������ĵ������ΪG����![]() ����
����![]() ����H��
����H��![]() ����
����![]() ����G��
����G��![]() ����
����![]() ����H��
����H��![]() ����
����![]() ����G����
����G����![]() ��
��![]() ����H��
����H��![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���BAC=90�㣬D��BC���е㣬E��AD���е�.����A��AF��BC����BE���ӳ����ڵ�F.
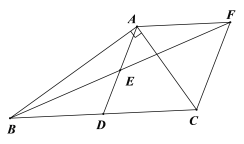
��1����֤����AEF�ա�DEB��
��2����AC=4��AB=5��������ADCF�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߿յ�����������ĸ߶��йأ�ij�ؾ����ĸ߶�ÿ����1km�������½�6�棬��֪��������Ϊ20��.
(1)д���õؿ�������T(��)��߶�h(km)֮��ĺ�������ʽ.
(2)����������4km��������T.
(3)������Ϊ-16�洦�����ĸ߶�h.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
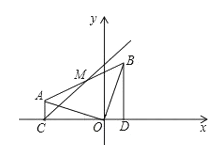
����Ŀ����ƽ��ֱ������ϵ����һ��BOD��![]() ���� BO �Ƶ�O ��ʱ����ת 90����OA�� ����AB����
���� BO �Ƶ�O ��ʱ����ת 90����OA�� ����AB����![]() �ڵ� C����B ������Ϊ��1��3��.
�ڵ� C����B ������Ϊ��1��3��.
��1����ֱ��AB �Ľ���ʽ��
��2����AB �е�Ϊ M������ CM������ P��Q ͬʱ�� C ��������� P ������CM ��ÿ��2����λ���ȵ��ٶ��˶�����Q���߶�CD ��ÿ��1����λ���ȵ��ٶ����յ� D �˶�����Q���˶���D ��ʱ��P��Qͬʱֹͣ�˶������PQO �����Ϊ S��![]() �����˶�ʱ��Ϊt�룬��S��t�ĺ�����ϵʽ����ֱ��д���Ա���t��ȡֵ��Χ��
�����˶�ʱ��Ϊt�룬��S��t�ĺ�����ϵʽ����ֱ��д���Ա���t��ȡֵ��Χ��
��3���ڣ�2���������£��Ƿ���������� P �㣬ʹ��P��O��BΪ�������������ֱ�������Σ������ڣ������Ӧ��t ֵ�ʹ�ʱQ������ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ����������������Ա��� x �뺯��ֵ y ���㣺��1��x��1 ʱ��1��y��1������������Ϊ���� ������.���磺y=x��y=x ���ǡ��պ�����. ��֪ y ax2 bx c(a0) �ǡ��պ��������������߾����� A(1��1)�͵� B(1��1)���� a ��ȡֵ��Χ��______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵxOy�У���ԭ��O����A��0��4����C��12��0��������OABC����AOC��ƽ���߽�AB�ڵ�D����P�ӵ�O��������ÿ��2![]() ����λ���ȵ��ٶ�������OD�����ƶ���ͬʱ��Q�ӵ�O��������ÿ��4����λ���ȵ��ٶ���x���������ƶ������ƶ�ʱ��Ϊt�룮
����λ���ȵ��ٶ�������OD�����ƶ���ͬʱ��Q�ӵ�O��������ÿ��4����λ���ȵ��ٶ���x���������ƶ������ƶ�ʱ��Ϊt�룮

��1������P�ƶ�����Dʱ�������ʱt��ֵ��
��2����tΪ��ֵʱ����PQBΪֱ�������Σ�
��3����֪��O��P��Q����������߽���ʽΪy=��![]() �����Ƿ����ijһʱ��t������PQB��ij����ת180���������Ӧ����ǡ�ö����������������ϣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�����Ƿ����ijһʱ��t������PQB��ij����ת180���������Ӧ����ǡ�ö����������������ϣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
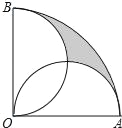
����Ŀ����ͼ���ڰ뾶Ϊ2cm��Բ�Ľ�Ϊ90�������OAB�У��ֱ���OA��OBΪֱ������Բ����ͼ����Ӱ���ֵ����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() �ϵ������㣬
�ϵ������㣬![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() ���ٶ����
���ٶ����![]() �˶���
�˶���![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() ���ٶ����
���ٶ����![]() �˶�����һ�㵽���յ�ʱ��
�˶�����һ�㵽���յ�ʱ��![]() ��
��![]() �����ͬʱֹͣ�˶������˶�ʱ��Ϊ
�����ͬʱֹͣ�˶������˶�ʱ��Ϊ![]() ��
��

��1����![]() �Ĵ���ʽ�ֱ��ʾ
�Ĵ���ʽ�ֱ��ʾ![]() ��
��![]() �ij���
�ij���
��2����![]() �����Ϊ
�����Ϊ![]() ��
��
����![]() �����
�����![]() ��
��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
����![]() ʱ��
ʱ��![]() �����
�����![]() �Ƕ��٣�
�Ƕ��٣�
��3����![]() Ϊ������ʱ���Ե�
Ϊ������ʱ���Ե�![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ�
���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������Ȥ�С����Χ��һ�����λ���������һ�߿�ǽ�����������ܳ�Ϊ![]() �����Χ�ɣ���֪ǽ��Ϊ
�����Χ�ɣ���֪ǽ��Ϊ![]() �ף���ͼ��ʾ���������������ֱ��ǽ��һ�߳�Ϊ
�ף���ͼ��ʾ���������������ֱ��ǽ��һ�߳�Ϊ![]() �ף�
�ף�

![]() �����������Ϊ
�����������Ϊ![]() ƽ���ף���
ƽ���ף���![]() ��
��
![]() ��ƽ����ǽ��һ�߳���С��
��ƽ����ǽ��һ�߳���С��![]() �ף������������������ֵ����Сֵ������У�������ֵ����Сֵ�����û�У���˵�����ɣ�
�ף������������������ֵ����Сֵ������У�������ֵ����Сֵ�����û�У���˵�����ɣ�
![]() ������������������
����������������С��![]() ƽ����ʱ��ֱ��д��
ƽ����ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com