
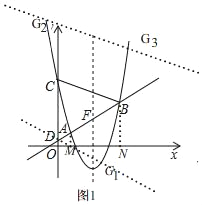
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ֱ��x=![]() �Գ����������y=ax2+bx+c��ֱ��l��y=kx+m��k��0������A��1��1����B���㣬��y�ύ��C��0��5����ֱ��l��y�ύ�ڵ�D��
�Գ����������y=ax2+bx+c��ֱ��l��y=kx+m��k��0������A��1��1����B���㣬��y�ύ��C��0��5����ֱ��l��y�ύ�ڵ�D��
��1���������ߵĺ�������ʽ��
��2����ֱ��l�������ߵĶԳ���Ľ���ΪF��G����������λ�ڶԳ����Ҳ��һ�㣬��![]() ������BCG����BCD�����ȣ����G�����ꣻ
������BCG����BCD�����ȣ����G�����ꣻ
��3������x�������ҽ���һ��P��ʹ��APB=90������k��ֵ��

���𰸡���1��y=x2��5x+5����2��G��3����1����G��![]() ��
��![]() ������3����1+
������3����1+![]()
��
��������
��1�����ݶ��κ�����ͼ����ϵ���Ĺ�ϵ�г���������a��b��c��ֵ���ö��κ����Ľ���ʽ��
��2����AM��x�ᣬBN��x�ᣬ����ֱ�ΪM��N���ɵó�B������꼴���г����������һ�κ�������ʽ���ٸ���S��BCD=S��BCG�г���ʽ�������G��
��3�����������г���ʽ���x��ֵ����B��k+4��k2+3k+1�����ٸ�����ABΪֱ����Բ��x��ֻ��һ�����㣬��PΪ�е㣬�ó�O��P��x�ᣬP��![]() ��0����������AMP�ס�PNB���ó�AMBN=PNPM��������ֵ�������k��ֵ.
��0����������AMP�ס�PNB���ó�AMBN=PNPM��������ֵ�������k��ֵ.
�⣺��1��������ɵ�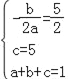 ��
��
���a=1��b=��5��c=5��
����κ����Ľ���ʽΪ��y=x2��5x+5��
��2����AM��x�ᣬBN��x�ᣬ����ֱ�ΪM��N��
��![]() ��
��
��MQ=![]() ��
��
��NQ=2��B��![]() ��
��![]() ����
����
��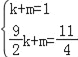 ��
��
���![]() ��
��
��![]() ��D��0��
��D��0��![]() ����
����
ͬ������![]() ��
��
��S��BCD=S��BCG��
���DG��BC��G��BC�·�����![]() ��
��
��![]() =x2��5x+5��
=x2��5x+5��
��ã�![]() ��x2=3��
��x2=3��
��x��![]() ��
��
��x=3��
��G��3����1����
��G��BC�Ϸ�ʱ��ֱ��G2G3��DG1����BC�Գƣ�
��![]() =
=![]() ��
��
![]() =x2��5x+5��
=x2��5x+5��
���![]() ��
��![]() ��
��
��x��![]() ��
��
��x=![]() ��
��
��G��![]() ��
��![]() ����
����
����������G������ΪG��3����1����G��![]() ��
��![]() ����
����
��3���������֪��k+m=1��
��m=1��k��
��yl=kx+1��k��
��kx+1��k=x2��5x+5��
��ã�x1=1��x2=k+4��
��B��k+4��k2+3k+1����
��AB�е�ΪO�䣬
��P������ֻ��һ����
����ABΪֱ����Բ��x��ֻ��һ�����㣬��PΪ�е㣬
��O��P��x�ᣬ
��PΪMN���е㣬
��P��![]() ��0����
��0����
�ߡ�AMP�ס�PNB��
��![]() ��
��
��AMBN=PNPM��
��1����k2+3k+1��=��k+4��![]() ����
����![]() ����
����
��k��0��
��k=![]() =��1+
=��1+![]() ��
��


 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȤС��ʱ����ʦ������������⣺
![]() ��ͼ
��ͼ![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ���ϵ�����
���ϵ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
С�������ھ��������������õ������µĽ���������ӳ�![]() ��
��![]() ��ʹ��
��ʹ��![]() ��������
��������![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ������
������![]() ��
��![]() ��
��![]() ������
������![]() �У����������ε����߹�ϵ�ɵ�
�У����������ε����߹�ϵ�ɵ�![]() ����
����![]() ��
��
[����]����ʱ�����������������е��������������������Կ��ǹ������е�Ϊ�Գ����ĵ����ĶԳ�ͼ�Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��е�ͬһ���������У�
![]() ������⣺�ܵ�
������⣺�ܵ�![]() ������������֤���������⣺��ͼ
������������֤���������⣺��ͼ![]() ����
����![]() ��
��![]() ��
��![]() ���ϵ��е㣬
���ϵ��е㣬![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ����֤��
����֤��![]() ����
����![]() ��̽���߶�
��̽���߶�![]() ��
��![]() ��
��![]() ֮��ĵ�����ϵ��������֤����
֮��ĵ�����ϵ��������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��y����![]() x+4��������ֱ��ཻ��A��B���㣬�ڵ�һ�����ڣ����߶�ABΪ��������������ABCD����A��C����ֱ��AC��
x+4��������ֱ��ཻ��A��B���㣬�ڵ�һ�����ڣ����߶�ABΪ��������������ABCD����A��C����ֱ��AC��

��1����գ���A���������� ����������ABCD�ı߳������� ����
��2����ֱ��AC�ĺ�������ʽ��
��3����ͼ2����һ����M��B��������1����λ����/����ٶ����յ�C�˶������˶���ʱ��Ϊt���룩������AM����tΪ��ֵʱ����AMƽ�֡�BAC����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ACB=90����AC=BC��DΪBC�е㣬CE��AD��E��BF��AC��CE���ӳ�����F��

��1����֤����ACD�ա�CBF��
��2����֤��AB��ֱƽ��DF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �����У�ÿ��С�����εı߳���Ϊ1����ͼ��ӴּӺ�.
�����У�ÿ��С�����εı߳���Ϊ1����ͼ��ӴּӺ�.
(1)ͼ�и��![]() �����Ϊ______.
�����Ϊ______.
(2)��ͼ�н����ʵ���ƽ��ֱ������ϵ��ʹ��![]() ��
��![]() .
.
(3)����![]() ����
����![]() ��ԳƵ�ͼ��
��ԳƵ�ͼ��![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt![]() �У���C=90����AC=BC�����߶�CB�ӳ�����ȡһ��P,��APΪֱ�DZߣ���PΪֱ�Ƕ��㣬������CB�Ϸ������� Rt
�У���C=90����AC=BC�����߶�CB�ӳ�����ȡһ��P,��APΪֱ�DZߣ���PΪֱ�Ƕ��㣬������CB�Ϸ������� Rt![]() , ����D��DE��CB,����Ϊ��E��
, ����D��DE��CB,������E��

��1�� �����ⲹȫͼ�Σ�
��2�� ��֤�� AC=PE��
��3�� ����DB�����ӳ���AC���ӳ����ڵ�F���õ�ʽ��ʾ�߶�CF��AC��������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����BAC=90������D�DZ�BC�ϵĶ��㣬����AD����C����ֱ��AD�ĶԳƵ�Ϊ��E������BE������AD���ڵ�F.


��1����ͼ1�У������ⲹȫͼ�Σ�
��2����![]() ��
��![]() ������
������![]() �Ĵ�С�����ú�
�Ĵ�С�����ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��3������ACE�ǵȱ������Σ�����EF��BC��������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����⽨һ��ƽ��ͼ��Ϊ���������Ϊ![]() ƽ����������ˮ�����أ�ƽ��ͼ��ͼ
ƽ����������ˮ�����أ�ƽ��ͼ��ͼ![]() ��ʾ�������ڵ������ƣ�������ˮ�����صij����������ܳ���
��ʾ�������ڵ������ƣ�������ˮ�����صij����������ܳ���![]() �ף�����ص���Χǽ���쵥��Ϊÿ��
�ף�����ص���Χǽ���쵥��Ϊÿ��![]() Ԫ���м�������ǽ���쵥��Ϊÿ��
Ԫ���м�������ǽ���쵥��Ϊÿ��![]() Ԫ���ص��쵥��Ϊÿƽ����
Ԫ���ص��쵥��Ϊÿƽ����![]() Ԫ������ǽ�ĺ�Ⱥ��Բ��ƣ�
Ԫ������ǽ�ĺ�Ⱥ��Բ��ƣ�
![]() ��������ˮ�����ص������Ϊ
��������ˮ�����ص������Ϊ![]() Ԫʱ����س�
Ԫʱ����س�![]() ��
��
![]() ����涨�����Խ�;�Խ���㣬��ô������Ŀ�ṩ����Ϣ����
����涨�����Խ�;�Խ���㣬��ô������Ŀ�ṩ����Ϣ����![]() ԪΪ���������������ˮ�������Ƿ�����㣿��˵�����ɣ�
ԪΪ���������������ˮ�������Ƿ�����㣿��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬��
���е㣬��![]() .
.![]() ��
��![]() ��һ���㣬��
��һ���㣬��![]() ����СֵΪ___________
����СֵΪ___________![]() .
.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com