
【题目】如图1,直线y=﹣![]() x+4与坐标轴分别相交于A、B两点,在第一象限内,以线段AB为边向外作正方形ABCD,过A、C点作直线AC.
x+4与坐标轴分别相交于A、B两点,在第一象限内,以线段AB为边向外作正方形ABCD,过A、C点作直线AC.

(1)填空:点A的坐标是 ,正方形ABCD的边长等于 ;
(2)求直线AC的函数解析式;
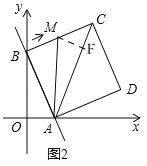
(3)如图2,有一动点M从B出发,以1个单位长度/秒的速度向终点C运动,设运动的时间为t(秒),连接AM,当t为何值时,则AM平分∠BAC?请说明理由.
【答案】(1)(3,0),5;(2)y=7x﹣21;(3)t为5![]() ﹣5时,AM平分∠BAC.
﹣5时,AM平分∠BAC.
【解析】
(1)根据坐标轴上点的特点求出点A,B坐标,即可得出结论;(2)先判断出△AOB≌△BNC,得出BN=OA=3,CN=OB=4,即可求出点C纵坐标,最后用待定系数法即可得出结论;(3)先判断出MF=CF,用CM=![]() BM建立方程即可得出结论;
BM建立方程即可得出结论;
解:
(1)∵直线y=![]() 与坐标轴分别相交于A、B两点,
与坐标轴分别相交于A、B两点,
令x=0,则y=4,
∴B(0,4),
令y=0,则0=![]() ,
,
∴x=3,
∴A(3,0),
∴AB=![]() =5,
=5,
故答案为:(3,0),5;
(2)如图1,过点C作CN⊥OB于N,
∴∠CBN+∠BCN=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠OBA+∠CBN=90°,
∴∠OBA=∠BCN,
在△AOB和△BNC中,
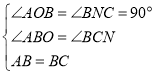 ,
,
∴△AOB≌△BNC(AAS),
∴CN=OB=4,BN=OA=3,
∴ON=OB+BN=7,
∴C(4,7),
设直线AC的解析式为y=kx+b,
∵A(3,0),
∴![]() ,
,
∴![]() ;
;
∴直线AC的解析式为y=7x﹣21;
(3)如图2,过M作MF⊥AC
当AM为∠BAC的角平分线时,
∵MF⊥AC,MB⊥AB
∴BM=FM
∵∠MCF=45°,
∴MF=CF
设BM=x,则CM=5﹣x,
则CM=![]() MF=
MF=![]() BM,
BM,
∴5﹣x=![]() x,
x,
∴(![]() +1)x=5,
+1)x=5,
∴x=![]() ,
,
∴t为![]() 时,AM平分∠BAC.
时,AM平分∠BAC.


科目:初中数学 来源: 题型:
【题目】蜀山区植物园是一座三面环水的半岛园区,拥有梅园、桂花园、竹园、木兰园、水景园等示范区。为了种植植物,需要从甲乙两地向园区A,B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A,B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需费用)。
运费(元/吨) | ||
A | B | |
甲地 | 12 | 12 |
乙地 | 10 | 8 |
运往A、B两地的吨数 | ||
A | B | |
甲地 | x | 50-x |
乙地 | ( ) | ( ) |
(1)设甲地运往A棚营养土x吨,请用关于x的代数式完成上表;
(2)设甲地运往A棚营养土x吨,求总运费y(元)关于x(吨)的函数关系式(要求写出变量取值范围);
(3)当甲、乙两地各运往A、B两棚多少吨营养土时,总运费最省?最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 内接于
内接于![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 的切线与
的切线与![]() 的延长线交于点
的延长线交于点![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长;
的长;
![]() 在题设条件下,为使
在题设条件下,为使![]() 是平行四边形,
是平行四边形,![]() 应满足怎样的条件(不要求证明).
应满足怎样的条件(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为5 厘米,对角线BD长8厘米.点P从点A出发沿AB方向匀速运动,速度为1厘米秒;点Q从点D 出发沿DB 方向匀速运动,速度为2 厘米/秒:P、Q 同时出发,当点Q与点B重合时,P、Q停止运动,设运动时间为t秒,解答下列问题:

(1)当t为何值时,△PBQ为等腰三角形?(2)当t为何值时,△PBQ的面积等于菱形ABCD面积的![]() ?
?
(3)连接AQ,在运动过程中,是否存在某一时刻t,使∠PQA=∠ABD?若存在,请求出t值; 若不存在,请说明理虫:
(4)直线PQ 交线段BC于点M,在运动过程中,是否存在某一时刻t,使BM:CM=2:3?若存在,请求出t值; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线y=x+2与两坐标轴分别交于A、B两点,点C是OB的中点,D、E分别是直线AB、y轴上的动点,当△CDE周长最小时,点D的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市里,某商户先后两次购进若干千克的黄瓜,第一次用了300元,第二次用了900元,但第二次的进货单价比第次的要高1.5元,而所购的黄瓜数量是第一次的2倍.
(1)问该商户两次一共购进了多少千克黄瓜?
(2)当商户按每千克6元的价格卖掉了![]() 时,商户想尽快卖掉这些黄瓜,于是商户决定将剩余的黄瓜打折销售,请你帮忙算算,剩余的黄瓜至少打几折才能使两次所进的黄瓜总盈利不低于360元?
时,商户想尽快卖掉这些黄瓜,于是商户决定将剩余的黄瓜打折销售,请你帮忙算算,剩余的黄瓜至少打几折才能使两次所进的黄瓜总盈利不低于360元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请作出△ABC关于y轴对称的△A1B1C1;
(2)△A1B1C1的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以直线x=![]() 对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y轴交于C(0,5),直线l与y轴交于点D.
对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y轴交于C(0,5),直线l与y轴交于点D.
(1)求抛物线的函数表达式;
(2)设直线l与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若![]() ,且△BCG与△BCD面积相等,求点G的坐标;
,且△BCG与△BCD面积相等,求点G的坐标;
(3)若在x轴上有且仅有一点P,使∠APB=90°,求k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:直线![]() 与直线
与直线![]() 外一点
外一点![]() .求作:过点
.求作:过点![]() 作直线
作直线![]() 的平行线.
的平行线.

已知:直线![]() 与直线
与直线![]() 外一点
外一点![]() .求作:过点
.求作:过点![]() 作直线
作直线![]() 的平行线.
的平行线.

小明的作法如下:
如图,

①在直线![]() 上任取两点
上任取两点![]() ,
,![]() ;
;
②以点![]() 为圆心,线段
为圆心,线段![]() 的长为半径作圆弧;
的长为半径作圆弧;
以点![]() 为圆心,线段
为圆心,线段![]() 的长为半径作圆弧;
的长为半径作圆弧;
两圆弧(与点![]() 在
在![]() 同侧)的交点为
同侧)的交点为![]() ;
;
③过点![]() ,
,![]() 作直线.
作直线.
所以直线![]() 即为所求.
即为所求.
如图,
①在直线![]() 上任取两点
上任取两点![]() ,
,![]() ;
;
②以点![]() 为圆心,线段
为圆心,线段![]() 的长为半径作圆弧;
的长为半径作圆弧;
以点![]() 为圆心,线段
为圆心,线段![]() 的长为半径作圆弧;
的长为半径作圆弧;
两圆弧(与点![]() 在
在![]() 同侧)的交点为
同侧)的交点为![]() ;
;
③过点![]() ,
,![]() 作直线.
作直线.
所以直线![]() 即为所求.
即为所求.
老师说:“小明的作法正确.”
请回答:(![]() )利用尺规作图完成小明的做法(保留作图痕迹);
)利用尺规作图完成小明的做法(保留作图痕迹);
(![]() )该作图的依据是__________.
)该作图的依据是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com