
【题目】如图所示,直线y=x+2与两坐标轴分别交于A、B两点,点C是OB的中点,D、E分别是直线AB、y轴上的动点,当△CDE周长最小时,点D的坐标为_____.

【答案】(﹣![]() ,
,![]() ).
).
【解析】
作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,由轴对称的性质,可得DF=DC,EC=EG,故当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF+DE+EG=FG,此时△DEC周长最小;
解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,
∵直线y=x+2与两坐标轴分别交于A、B两点,点C是OB的中点,
∴B(﹣2,0),C(﹣1,0),
∴BO=2,OG=1,BG=3,
易得∠ABC=45°,
∴△BCF是等腰直角三角形,
∴BF=BC=1,
由轴对称的性质,可得DF=DC,EC=EG,
当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF+DE+EG=FG,
此时△DEC周长最小,
设直线FG的解析式为:y=kx+b,
∵F(﹣2,1),G(1,0),
∴![]() ,
,
∴![]() ,
,
直线FG的解析式为:![]() ,
,
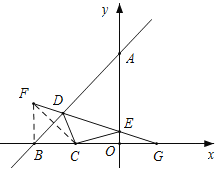
解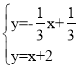 得
得![]() ,
,
∴点D的坐标为(﹣![]() ,
,![]() ),
),
故答案为:(﹣![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从
某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)
与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:
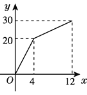
①每分钟进水5升;②当4≤x≤12时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以上说法中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,对于下列结论:①
,对于下列结论:①![]() ;②
;②![]() ;③弧
;③弧![]() 弧
弧![]() ;④
;④![]() 为
为![]() 的切线,结论一定正确的是( )
的切线,结论一定正确的是( )

A. ②③ B. ②④ C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,点M、N分别是AB、AC上的点,且AM=AN.连接MN、CM、BN,点D、E、F、G分别是BC、MN、BN、CM的中点,连接E、F、D、G.
(l)判断四边形EFDG的形状是 (不必证明);
(2)现将△AMN绕点A旋转一定的角度,其他条件不变(如图②),四边形EFDG的形状是否发生变化?证明你的结论;
(3)如图②,在(2)的情况下,请将△ABC在原有的条件下添加一个条件,使四边形EFDG是正方形.请写出你添加的条件,并在添加条件的基础上证明四边形EFDG是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 和
和![]() 中,
中, ![]() ,
,![]() ,
,![]() .
.

(1)若![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
(2)在第(1)问的条件下,求证: ![]() ;
;
(3)将![]() 绕点
绕点![]() 顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=﹣![]() x+4与坐标轴分别相交于A、B两点,在第一象限内,以线段AB为边向外作正方形ABCD,过A、C点作直线AC.
x+4与坐标轴分别相交于A、B两点,在第一象限内,以线段AB为边向外作正方形ABCD,过A、C点作直线AC.

(1)填空:点A的坐标是 ,正方形ABCD的边长等于 ;
(2)求直线AC的函数解析式;
(3)如图2,有一动点M从B出发,以1个单位长度/秒的速度向终点C运动,设运动的时间为t(秒),连接AM,当t为何值时,则AM平分∠BAC?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午”节前,第一次爸爸去超市购买了大小、质量都相同的火腿粽子和豆沙粽子若干,放入不透明的盒中,此时随机取出火腿粽子的概率为![]() ;妈妈发现小亮喜欢吃的火腿粽子偏少,第二次妈妈又去买了同样的
;妈妈发现小亮喜欢吃的火腿粽子偏少,第二次妈妈又去买了同样的![]() 只火腿粽子和
只火腿粽子和![]() 只豆沙粽子放入同一盒中,这时随机取出火腿粽子的概率为
只豆沙粽子放入同一盒中,这时随机取出火腿粽子的概率为![]() .
.
![]() 请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只?
请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只?
![]() 若妈妈从盒中取出火腿粽子
若妈妈从盒中取出火腿粽子![]() 只、豆沙粽子
只、豆沙粽子![]() 只送爷爷和奶奶后,再让小亮从盒中不放回地任取
只送爷爷和奶奶后,再让小亮从盒中不放回地任取![]() 只,问恰有火腿粽子、豆沙粽子各
只,问恰有火腿粽子、豆沙粽子各![]() 只的概率是多少?(用字母和数字表示豆沙粽子和火腿粽子,用列清法计算)
只的概率是多少?(用字母和数字表示豆沙粽子和火腿粽子,用列清法计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 网格中,每个小正方形的边长都为1,画图请加粗加黑.
网格中,每个小正方形的边长都为1,画图请加粗加黑.
(1)图中格点![]() 的面积为______.
的面积为______.
(2)在图中建立适当的平面直角坐标系,使点![]() ,
,![]() .
.
(3)画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读“末位数字是![]() 的两位数平方的速算法则”,并完成下列问题.
的两位数平方的速算法则”,并完成下列问题.
通过计算器计算可得:![]() .容易发现这样的速算法则:末位数字是
.容易发现这样的速算法则:末位数字是![]() 的两位数的平方,可以先写出它的十位数字与其下一个自然数的乘积,再在末位接着写上
的两位数的平方,可以先写出它的十位数字与其下一个自然数的乘积,再在末位接着写上![]() .例如:计算
.例如:计算![]() ,因为
,因为![]() ,在
,在![]() 的后面接着写上
的后面接着写上![]() ,所以
,所以![]() ;计算
;计算![]() ;因为
;因为![]() ,在
,在![]() 的后面接着写上
的后面接着写上![]() ,所以
,所以![]() .
.
(1)用学过的整式的乘法来验证“末位数字是![]() 的两位数平方的速算法则”是否正确:
的两位数平方的速算法则”是否正确:
第一步:我们设末位数字是![]() 的两位数中的十位数字为
的两位数中的十位数字为![]() ,这个两位数用含
,这个两位数用含![]() 的代数式表示为_____,则它的平方为 ( 请把平方结果计算出来并化简);
的代数式表示为_____,则它的平方为 ( 请把平方结果计算出来并化简);
第二步:依据文中“先写出它的十位数字与其下一个自然数的乘积,再在末位接着写上25"这一句话,用含n的代数式表示速算计算结果为 ,这个代数式化简后为 ;
第三步:因为第一步和第二步最终得到的代数式结果相等,所以得出速算法则是“正确”的结论
(2)如果计算的是末位数字是![]() 的三位数、四位数···,这个速算法则 (填“成立”或“不成立”).
的三位数、四位数···,这个速算法则 (填“成立”或“不成立”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com