
【题目】如图,△ABC中,∠C=90°,AC=BC,D、E分别在AC、BC上,若∠DBC=2∠BAE,AB=4![]() ,CD=
,CD=![]() ,则CE的长为_____.
,则CE的长为_____.
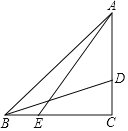
【答案】2![]()
【解析】
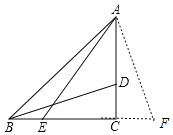
如图,延长BC至F,使CF=CD=![]() ,连接AF,由等腰直角三角形的性质可得AC=BC=4,∠ABC=∠BAC=45°,由勾股定理可求AF=
,连接AF,由等腰直角三角形的性质可得AC=BC=4,∠ABC=∠BAC=45°,由勾股定理可求AF=![]() ,由“SAS”可证△ACF≌△BCD,可得∠CAF=∠CBD=2α,可求∠EAF=45°﹣α+2α=45°+α=∠AEF,可得AF=EF,即可求解.
,由“SAS”可证△ACF≌△BCD,可得∠CAF=∠CBD=2α,可求∠EAF=45°﹣α+2α=45°+α=∠AEF,可得AF=EF,即可求解.
解:如图,延长BC至F,使CF=CD=![]() ,连接AF,
,连接AF,
∵∠C=90°,AC=BC,AB=4![]() ,
,
∴AC=BC=4,∠ABC=∠BAC=45°,
∴AF=![]() ,
,
设∠BAE=α,则∠DBC=2α,
∴∠AEF=∠ABC+∠BAE=45°+α,∠EAC=45°﹣α
∵BC=AC,∠BCD=∠ACF=90°,CD=CF,
∴△ACF≌△BCD(SAS)
∴∠CAF=∠CBD=2α,
∴∠EAF=45°﹣α+2α=45°+α=∠AEF,
∴AF=EF=![]() ,
,
∴EC=EF﹣CF=![]() ,
,
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】已知点![]() 是等腰直角三角形
是等腰直角三角形![]() 斜边上的中点,
斜边上的中点,![]() ,
,![]() 是
是![]() 上一点,连结
上一点,连结![]() .
.
(1)如图1,若点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,若点![]() 在
在![]() 延长线上,
延长线上,![]() ,垂足为
,垂足为![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,其它条件不变,则结论“
,其它条件不变,则结论“![]() ”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
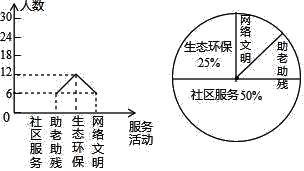
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:![]() ;
;
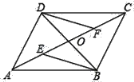
(2)如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DE∥BE,求证:△BOE≌△DOF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指出其他垃圾,小明、小亮各投放了一袋垃圾.
(1)直接写出小明投放的垃圾恰好是A类的概率;
(2)求小亮投放的垃圾与小明投放的垃圾是同一类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
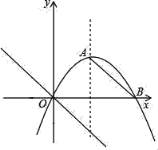
【题目】如图,抛物线y=ax2+2x与x轴相交于点B,其对称轴为x=3.
(1)求直线AB的解析式;
(2)过点O作直线l,使l∥AB,点P是l上一动点,设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t,当0<S≤18时,求t的取值范围;
(3)在(2)的条件下,当t取最大值时,抛物线上是否存在点Q,使△OPQ为直角三角形且OP为直角边,若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天早上小华步行上学,他离开家后不远便发现数学书忘在了家里,于是以相同的速度回家去拿,到家后发现弟弟把牛奶洒在了地上,就放下手中的东西,收拾好后才离开.为了不迟到,小华跑步到了学校,则小华离学校的距离y与时间t之间的函数关系的大致图象是( )
A.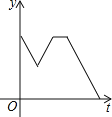 B.
B.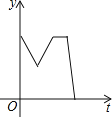 C.
C.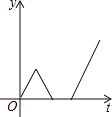 D.
D.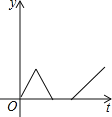
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.三角形的三条高线相交于三角形内一点
B.等腰三角形的中线与高线重合
C.三边长为![]() 的三角形为直角三角形
的三角形为直角三角形
D.到线段两端距离相等的点在这条线段的垂直平分线上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com