
【题目】一天早上小华步行上学,他离开家后不远便发现数学书忘在了家里,于是以相同的速度回家去拿,到家后发现弟弟把牛奶洒在了地上,就放下手中的东西,收拾好后才离开.为了不迟到,小华跑步到了学校,则小华离学校的距离y与时间t之间的函数关系的大致图象是( )
A.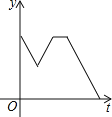 B.
B.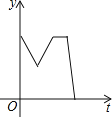 C.
C.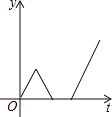 D.
D.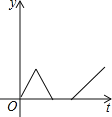
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=4,BC=5,AC的长是一元二次方程x2﹣15x+54=0的一个根.
(1)求AC的长;
(2)在AC上找一点D,连接BD,使△ABD∽△ACB;
(3)以AC为一边作一个三角形ACM,求出sin∠AMC的值.(所作三角形自己设计)
查看答案和解析>>
科目:初中数学 来源: 题型:
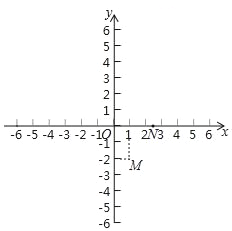
【题目】已知抛物线y=ax2+bx+c(x为任意实数)经过下图中两点M(1,﹣2)、N(m,0),其中M为抛物线的顶点,N为定点.下列结论:
①若方程ax2+bx+c=0的两根为x1,x2(x1<x2),则﹣1<x1<0,2<x2<3;
②当x<m时,函数值y随自变量x的减小而减小.
③a>0,b<0,c>0.
④垂直于y轴的直线与抛物线交于C、D两点,其C、D两点的横坐标分别为s、,则s+t=2.
其中正确的是( )
A. ①② B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过圆外一点作圆的切线”的尺规作图的过程.
已知:P为外一点.求作:经过P点的切线.作法:如图,(1)连结OP;(2)以OP为直径作圆,与交于C、D两点.(3)作直线PC、PD.则直线PC、PD就是所求作经过P点的切线.以上作图的依据是:_____.
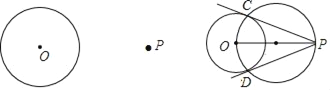
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
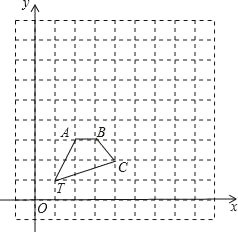
【题目】如图,在正方形网格中,四边形TABC的顶点坐标分别为T(1,1),A(2,3),B(3,3),C(4,2).
(1)以点T(1,1)为位似中心,在位似中心的同侧将四边形TABC放大为原来的2倍,放大后点A,B,C的对应点分别为A′,B′,C′画出四边形TA′B′C′;
(2)写出点A′,B′,C′的坐标:
A′ ,B′ ,C′ ;
(3)在(1)中,若D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com