
【题目】已知△ABC中,AB=4,BC=5,AC的长是一元二次方程x2﹣15x+54=0的一个根.
(1)求AC的长;
(2)在AC上找一点D,连接BD,使△ABD∽△ACB;
(3)以AC为一边作一个三角形ACM,求出sin∠AMC的值.(所作三角形自己设计)
【答案】(1)AC=6;(2)见解析;当AD=![]() 时,△ABD∽△ACB;(3)sin∠AMC=
时,△ABD∽△ACB;(3)sin∠AMC=![]() .
.
【解析】
(1)解一元二次方程x2-15x+54=0,可得x1=6,x2=9,再根据三角形的三边关系,即可得到AC的范围,进而得出AC的长;
(2)依据相似三角形的对应边成比例,即可得到AD的长,即可得出点D的位置;
(3)以AC为一边作一个等边三角形ACM,即可得到sin∠AMC的值,答案不唯一.
(1)解一元二次方程x2﹣15x+54=0,可得
x1=6,x2=9,
∵5﹣4<AC<5+4,
∴1<AC<9,
∵AC的长是一元二次方程x2﹣15x+54=0的一个根,
∴AC=6;
(2)如图所示,当△ABD∽△ACB时,
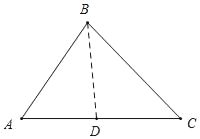
![]() =
=![]() ,即AB2=AD×AC,
,即AB2=AD×AC,
∴16=AD×6,
∴AD=![]() ,
,
∴当AD=![]() 时,△ABD∽△ACB;
时,△ABD∽△ACB;
(3)如图所示,以AC为一边作一个等边三角形ACM,则∠AMC=60°,
∴sin∠AMC=sin60°=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
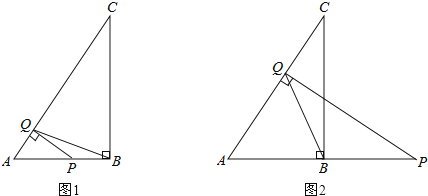
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
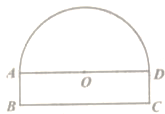
【题目】如图,隧道的截面由半圆和长方形构成,长方形的长BC为8m,宽AB为1m,该隧道内设双向行驶的车道(共有2条车道),若现有一辆货运卡车高4m,宽2.3m。则这辆货运卡车能否通过该隧道?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 是等腰直角三角形
是等腰直角三角形![]() 斜边上的中点,
斜边上的中点,![]() ,
,![]() 是
是![]() 上一点,连结
上一点,连结![]() .
.
(1)如图1,若点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,若点![]() 在
在![]() 延长线上,
延长线上,![]() ,垂足为
,垂足为![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,其它条件不变,则结论“
,其它条件不变,则结论“![]() ”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
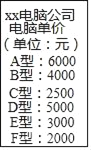
【题目】某电脑公司现有A,B,C,D四种型号的甲品牌电脑和E、F两种型号的乙品牌电脑.实验中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写出所有选购方案;
(2)如果(1)中各种选购方案被选中的可能性相等,那么A型电脑被选中的概率是多少?A型与E型号被同时选中的概率是多少?
(3)现知实验中学购买甲、乙两种品牌电脑共10台(价格如图所示),恰好用了4万元人民币,其中甲品牌电脑为A型号电脑,那么购买A型号电脑有几台?.
查看答案和解析>>
科目:初中数学 来源: 题型:
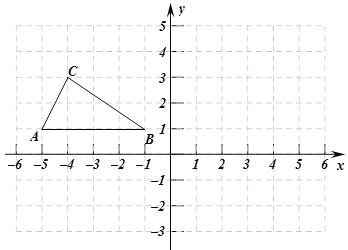
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-5,1),B(-1,1),C(-4,3).
(1)若△A1B1C1与△ABC关于y轴对称,点A,B,C的对应点分别为A1,B1,C1,请画出△A1B1C1并写出A1,B1,C1的坐标;
(2)若点P为平面内不与C重合的一点,△PAB与△ABC全等,请写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以点P为端点竖直向下的一条射线PN,以它为对称轴向左右对称摆动形成了射线PN1,PN2,我们规定:∠N1PN2为点P的“摇摆角”,射线PN摇摆扫过的区域叫作点P的“摇摆区域”(含PN1,PN2).
在平面直角坐标系xOy中,点P(2,3).
(1)当点P的摇摆角为60°时,请判断O(0,0)、A(1,2)、B(2,1)、C(2+![]() ,0)属于点P的摇摆区域内的点是 (填写字母即可);
,0)属于点P的摇摆区域内的点是 (填写字母即可);
(2)如果过点D(1,0),点E(5,0)的线段完全在点P的摇摆区域内,那么点P的摇摆角至少为 °;
(3)⊙W的圆心坐标为(a,0),半径为1,如果⊙W上的所有点都在点P的摇摆角为60°时的摇摆区域内,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
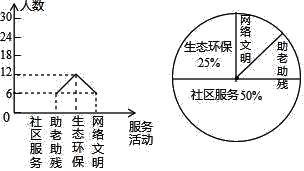
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天早上小华步行上学,他离开家后不远便发现数学书忘在了家里,于是以相同的速度回家去拿,到家后发现弟弟把牛奶洒在了地上,就放下手中的东西,收拾好后才离开.为了不迟到,小华跑步到了学校,则小华离学校的距离y与时间t之间的函数关系的大致图象是( )
A.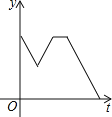 B.
B.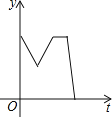 C.
C.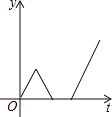 D.
D.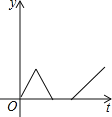
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com