
【题目】以点P为端点竖直向下的一条射线PN,以它为对称轴向左右对称摆动形成了射线PN1,PN2,我们规定:∠N1PN2为点P的“摇摆角”,射线PN摇摆扫过的区域叫作点P的“摇摆区域”(含PN1,PN2).
在平面直角坐标系xOy中,点P(2,3).
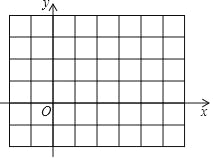
(1)当点P的摇摆角为60°时,请判断O(0,0)、A(1,2)、B(2,1)、C(2+![]() ,0)属于点P的摇摆区域内的点是 (填写字母即可);
,0)属于点P的摇摆区域内的点是 (填写字母即可);
(2)如果过点D(1,0),点E(5,0)的线段完全在点P的摇摆区域内,那么点P的摇摆角至少为 °;
(3)⊙W的圆心坐标为(a,0),半径为1,如果⊙W上的所有点都在点P的摇摆角为60°时的摇摆区域内,求a的取值范围.
【答案】(1) B、C;(2)90°;(3)2﹣![]() ≤a≤2+
≤a≤2+![]() .
.
【解析】
(1)根据题意作出图象,从而得到答案;
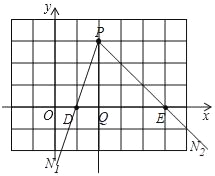
(2)如图所示,当射线PN1过点D时,由对称性可知,此时点E不在点P的摇摆区域内,
当射线PN2过点E时,由对称性可知,此时点D在点P的摇摆区域内,易知:此时PQ=QE,从而得到∠EPQ的度数,从而得到答案;
(3)设直线PN1与x轴交于点M,⊙W与射线PN1相切于点N,P为端点竖直向下的一条射线PN与x轴交于点Q,由题意可知:∠PMW=60°,利用三角函数求出MW,MQ的值,从而得到OM,OW的值,得到两个W的坐标,从而得到a的取值范围.
解:(1)根据“摇摆角”作出图形,如图所示,
将O、A、B、C四点在平面直角坐标系中描出,后,
可以发现,B、C在点P的摇摆区域内,
故属于点P的摇摆区域内的点是B、C
(2)如图所示,当射线PN1过点D时,
由对称性可知,此时点E不在点P的摇摆区域内,
当射线PN2过点E时,
由对称性可知,此时点D在点P的摇摆区域内,
易知:此时PQ=QE,
∴∠EPQ=45°,
∴如果过点D(1,0),点E(5,0)的线段完全在点P的摇摆区域内,那么点P的摇摆角至少为90°
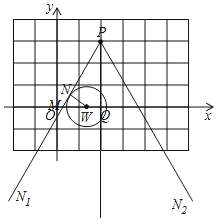
(3)如果⊙W上的所有点都在点P的摇摆角为60°时的摇摆区域内,
此时⊙W与射线PN1相切,
设直线PN1与x轴交于点M,⊙W与射线PN1相切于点N,P为端点竖直向下的一条射线PN与x轴交于点Q,
由定义可知:∠PMW=60°,
∵NW=1,PQ=3,
∴sin∠PMW=![]() ,tan∠PMW=
,tan∠PMW=![]()
∴MW=![]() ,MQ=
,MQ=![]() ,
,
∴OM=2﹣![]() ,
,
∴OW=OM+MW=2﹣![]() +
+![]() =2﹣
=2﹣![]()
∴此时W的坐标为:(2﹣![]() ,0)
,0)
由对称性可知:当⊙W与射线PN2相切时,
此时W的坐标为:(2+![]() ,0)
,0)
∴a的范围为:2﹣![]() ≤a≤2+
≤a≤2+![]()


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】从宁海县到某市,可乘坐普通列车或高铁,已知高铁的行驶路程与普通列车的行驶路程之和是920千米,而普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车的平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:河上有一座抛物线形桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB=6m,建立如图所示的坐标系.
(1)当水位上升0.5m时,求水面宽度CD为多少米?(结果可保留根号)
(2)有一艘游船它的左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在上述河流中航行,若这船宽(最大宽度)2米,从水面到棚顶高度为1.8米.问这艘船能否从桥下洞通过?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=4,BC=5,AC的长是一元二次方程x2﹣15x+54=0的一个根.
(1)求AC的长;
(2)在AC上找一点D,连接BD,使△ABD∽△ACB;
(3)以AC为一边作一个三角形ACM,求出sin∠AMC的值.(所作三角形自己设计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB交AB于点D;∠CAE=∠B.
(1)如果AC=3.5 cm,求AB的长度;
(2)猜想:ED与AB的位置关系,并证明你的猜想。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过圆外一点作圆的切线”的尺规作图的过程.
已知:P为外一点.求作:经过P点的切线.作法:如图,(1)连结OP;(2)以OP为直径作圆,与交于C、D两点.(3)作直线PC、PD.则直线PC、PD就是所求作经过P点的切线.以上作图的依据是:_____.
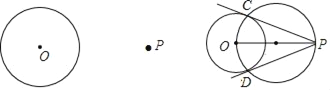
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com