
【题目】已知点![]() 是等腰直角三角形
是等腰直角三角形![]() 斜边上的中点,
斜边上的中点,![]() ,
,![]() 是
是![]() 上一点,连结
上一点,连结![]() .
.
(1)如图1,若点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,若点![]() 在
在![]() 延长线上,
延长线上,![]() ,垂足为
,垂足为![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,其它条件不变,则结论“
,其它条件不变,则结论“![]() ”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

【答案】(1)证明见解析;(2)成立,证明见解析.
【解析】
(1)根据等腰直角三角形的性质和全等三角形的判定得出Rt△BOE≌Rt△AOF,进而证明即可.
(2)根据等腰直角三角形的性质和全等三角形的判定得出Rt△BOE≌Rt△AOF,进而解答即可.
(1)证明:∵三角形ABC是等腰直角三角形,AB=BC,
∴∠BAC=∠ACB=45°
又点O是AC边上的中点,
∴∠BOE=∠AOF=90°,∠ABO=∠CBO=45°
∴∠BAC=∠ABO,
∴OB=OA,
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO,
∴Rt△BOE≌Rt△AOF,
∴OE=OF;
(2)OE=OF成立;
∵三角形ABC是等腰直角三角形,AB=BC,
∴∠BAC=∠ACB=45°
又点O是AC边上的中点,
∴∠BOE=∠AOF=90°,∠ABO=∠CBO=45°
∴∠BAC=∠ABO,
∴OB=OA,
又∵AM⊥BE,
∴∠F+∠MBF=90°=∠B+∠OBE,
又∵∠MBF=∠OBE,
∴∠F=∠E,
∴Rt△BOE≌Rt△AOF,
∴OE=OF


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图![]() ,
,![]() ,那么
,那么![]() 成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.
成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.
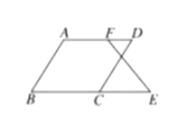
解:成立,理由如下:
![]() (已知)
(已知)
![]() ① (同旁内角互补,两条直线平行)
① (同旁内角互补,两条直线平行)
![]() (② )
(② )
又![]()
![]() (已知),
(已知),![]() (等量代换)
(等量代换)
![]() (③ )
(③ )
![]() (④ ).
(④ ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() (a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
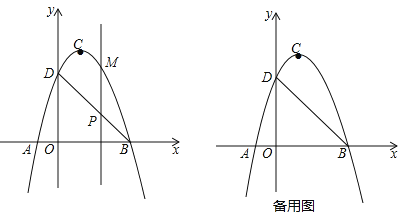
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为![]() ?若存在求出点Q的坐标;若不存在请说明理由.
?若存在求出点Q的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:河上有一座抛物线形桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB=6m,建立如图所示的坐标系.
(1)当水位上升0.5m时,求水面宽度CD为多少米?(结果可保留根号)
(2)有一艘游船它的左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在上述河流中航行,若这船宽(最大宽度)2米,从水面到棚顶高度为1.8米.问这艘船能否从桥下洞通过?

查看答案和解析>>
科目:初中数学 来源: 题型:
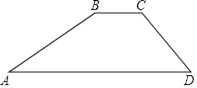
【题目】如图,一水库大坝的横断面为梯形ABCD,坝顶宽6米,坝高10米,斜坡AB的坡度i1=1:3,斜坡CD的坡度i2=1:1.
(1)求斜坡AB的长(结果保留根号);
(2)求坝底AD的长度;
(3)求斜坡CD的坡角α.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=4,BC=5,AC的长是一元二次方程x2﹣15x+54=0的一个根.
(1)求AC的长;
(2)在AC上找一点D,连接BD,使△ABD∽△ACB;
(3)以AC为一边作一个三角形ACM,求出sin∠AMC的值.(所作三角形自己设计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com