
【题目】如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证:
(1)△ABD≌△BCE;
(2)△AEF∽△ABE.
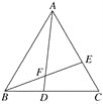
【答案】(1)见解析;(2)见解析.
【解析】
(1)由△ABC 是等边三角形,根据等边三角形的性质可得: AB=BC , ∠ABD=∠C=∠BAC=60°,继而根据SAS即可证得△ABD≌△BCE ;
(2)由△ABD≌△BCE ,可证得∠BAD=∠CBE ,进一步得到∠EAF=∠ABE ,然后根据有两角对应相等的三角形相似,即可得△AEF∽△ABE .
证明 (1)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=∠BAC=60°,
在△ABD和△BCE中,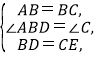
∴△ABD≌△BCE(SAS);
(2)∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠EAF=∠ABE,
∵∠AEF=∠BEA,
∴△AEF∽△ABE.


科目:初中数学 来源: 题型:
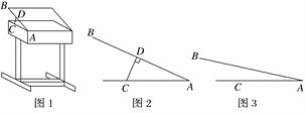
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
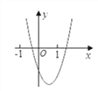
【题目】二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )
A.  B.
B.  C.
C. 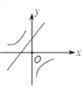 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程m x2-(m+2)x+2=0(m≠0).
(1)求证:无论m为何值时,这个方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)__________米.
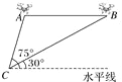
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.

(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan53°≈1.33, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+4与反比例函数y=![]() 的图象相交于A(-3,a)和B两点.
的图象相交于A(-3,a)和B两点.
(1)求k的值;
(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;
(3)直接写出不等式![]() >x的解集.
>x的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小玲为毕业联欢会设计了一个“配橙色”的游戏,使用的是如图所示两个可以自由转动的转盘,每个转盘被分成面积相等的若干个扇形,不同扇形分别填涂颜色,分界线可忽略,游戏者同时转动两个转盘,两个转盘停止转动时,若有一个转盘的指针指向红色,另一个转盘的指针指向黄色,则“配橙色”游戏成功,游戏者获胜.求游戏者获胜的概率.(用列表法或画树状图说明)
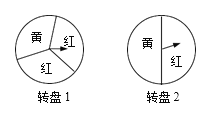
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com