
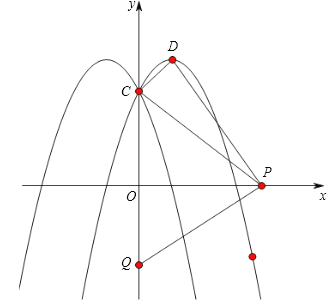
【题目】已知二次函数y=ax2﹣2ax+c(a<0)的最大值为4,且抛物线过点(![]() ,﹣
,﹣![]() ),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
(1)求该二次函数的解析式,及顶点D的坐标;
(2)求|PC﹣PD|的最大值及对应的点P的坐标;
(3)设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点,求t的取值.
【答案】(1)![]() ,D(1,4);(2)
,D(1,4);(2)![]() ,P(﹣3,0);(3)t的取值是
,P(﹣3,0);(3)t的取值是![]() ≤t<3或t=
≤t<3或t=![]() 或t≤﹣3.
或t≤﹣3.
【解析】
试题(1)先利用对称轴公式x=![]() 计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
(2)根据三角形的三边关系:可知P、C、D三点共线时|PC﹣PD|取得最大值,求出直线CD与x轴的交点坐标,就是此时点P的坐标;
(3)先把函数中的绝对值化去,可知![]() ,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数
,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数![]() (x≥0)时有一个公共点时,求t的值;③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ与当函数
(x≥0)时有一个公共点时,求t的值;③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ与当函数![]() (x<0)时也有一个公共点,则当t≤﹣3时,都满足条件;综合以上结论,得出t的取值.
(x<0)时也有一个公共点,则当t≤﹣3时,都满足条件;综合以上结论,得出t的取值.
(1)∵![]() 的对称轴为:x=1,∴抛物线过(1,4)和(
的对称轴为:x=1,∴抛物线过(1,4)和(![]() ,
,![]() )两点,代入解析式得:
)两点,代入解析式得: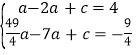 ,解得:a=﹣1,c=3,∴二次函数的解析式为:
,解得:a=﹣1,c=3,∴二次函数的解析式为:![]() ,∴顶点D的坐标为(1,4);
,∴顶点D的坐标为(1,4);
(2)∵C、D两点的坐标为(0,3)、(1,4);
由三角形两边之差小于第三边可知:
|PC﹣PD|≤|CD|,∴P、C、D三点共线时|PC﹣PD|取得最大值,此时最大值为,|CD|=![]() ,由于CD所在的直线解析式为y=x+3,将P(t,0)代入得t=﹣3,∴此时对应的点P为(﹣3,0);
,由于CD所在的直线解析式为y=x+3,将P(t,0)代入得t=﹣3,∴此时对应的点P为(﹣3,0);
(3)![]() 的解析式可化为:
的解析式可化为:
![]()
设线段PQ所在的直线解析式为y=kx+b,将P(t,0),Q(0,2t)代入得:
线段PQ所在的直线解析式:y=﹣2x+2t,分三种情况讨论:
①当线段PQ过点(0,3),即点Q与点C重合时,线段PQ与函数![]() 有一个公共点,此时t=
有一个公共点,此时t=![]() ,当线段PQ过点(3,0),即点P与点(3,0)重合时,t=3,此时线段PQ与
,当线段PQ过点(3,0),即点P与点(3,0)重合时,t=3,此时线段PQ与![]() 有两个公共点,所以当
有两个公共点,所以当![]() ≤t<3时,线段PQ与
≤t<3时,线段PQ与![]() 有一个公共点;
有一个公共点;
②将y=﹣2x+2t代入![]() (x≥0)得:
(x≥0)得:
![]() ,
,![]() ,令△=16﹣4(﹣1)(3﹣2t)=0,t=
,令△=16﹣4(﹣1)(3﹣2t)=0,t=![]() >0,所以当t=
>0,所以当t=![]() 时,线段PQ与
时,线段PQ与![]() 也有一个公共点;
也有一个公共点;
③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ只与![]() (x<0)有一个公共点,此时t=﹣3,所以当t≤﹣3时,线段PQ与
(x<0)有一个公共点,此时t=﹣3,所以当t≤﹣3时,线段PQ与![]() 也有一个公共点,综上所述,t的取值是
也有一个公共点,综上所述,t的取值是![]() ≤t<3或t=
≤t<3或t=![]() 或t≤﹣3.
或t≤﹣3.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】 已知:如图1,在Rt△ABC和Rt△A′B′C′中,AB=A′B′,AC=A′C′,∠C=∠C′=90°.求证:Rt△ABC和Rt△A′B′C′全等.
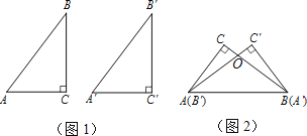
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)如图2,将△ABC和A′B′C′拼在一起(即:点A与点B′重合,点B与点A′重合),BC和B′C′相交于点O,请用此图证明上述命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
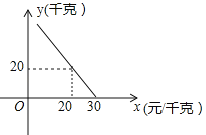
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
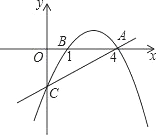
【题目】如图,抛物线y1=﹣![]() x2+bx+c经过点A(4,0)和B(1,0),与y轴交于点C.
x2+bx+c经过点A(4,0)和B(1,0),与y轴交于点C.
(1)求出抛物线的解析式;
(2)求点C的坐标及抛物线的顶点坐标;
(3)设直线AC的解析式为y2=mx+n,请直接写出当y1<y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
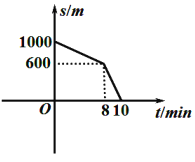
【题目】放学后,小刚和同学边聊边往家走,突然想起今天是妈妈的生日,赶紧加快速度,跑步回家.小刚离家的距离![]() 和放学后的时间
和放学后的时间![]() 之间的关系如图所示,给出下列结论:①小刚家离学校的距离是
之间的关系如图所示,给出下列结论:①小刚家离学校的距离是![]() ;②小刚跑步阶段的速度为
;②小刚跑步阶段的速度为![]() ;③小刚回到家时已放学10分钟;④小刚从学校回到家的平均速度是
;③小刚回到家时已放学10分钟;④小刚从学校回到家的平均速度是![]() .其中正确的个数是( )
.其中正确的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com