
【题目】如图,△ABC中,AB=BC,∠ABC=120°,点E是AC上一点,连接BE,且∠BEC=50°,D为点B关于直线AC的对称点,连接CD,将线段EB绕点E顺时针旋转40°得到线段EF,连接DF.
(1)请你在下图中补全图形;
(2)请写出∠EFD的大小,并说明理由;
(3)连接CF,求证:DF=CF.

【答案】(1)图见解析;(2)60°;理由见解析;(3)见解析.
【解析】
(1)根据题意补全图形即可;
(2)连接ED,根据对称性质可得:ED=EB,∠BEC=∠DEC=50°,再根据旋转性质可得:BE=EF,∠BEF=40°,从而得出EF=ED,∠FED=∠BEC+∠DEC-∠BEF=60°,即可判定△EFD为等边三角形,从而求出∠EFD的大小;
(3)连接BF并延长交DC于G,利用等边对等角求出∠BCA,根据对称的性质可得:CB=CD,∠BCG=2∠BAC=2∠DCA=60°,再求出∠CBG的度数,从而可判定BG⊥CD,再根据30°所对的直角边是斜边的一半,即可证出G是CD的中点,从而得到BG垂直平分CD,根据垂直平分线的性质即可证DF=CF.
补全图形如下所示:
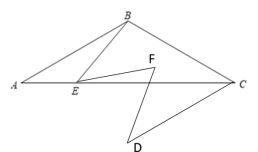
(2)连接ED,
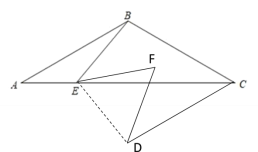
∵D为点B关于直线AC的对称点
∴ED=EB,∠BEC=∠DEC=50°
∵EB绕点E顺时针旋转40°得到线段EF
∴BE=EF,∠BEF=40°
∴EF=ED,∠FED=∠BEC+∠DEC-∠BEF=60°
∴△EFD为等边三角形
∴∠EFD=60°
(3)连接BF并延长交DC于G
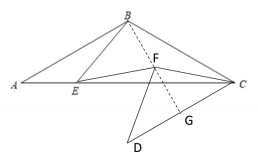
∵AB=AC,∠ABC=120°
∴∠A=∠BCA=![]() (180°-∠ABC)=30°
(180°-∠ABC)=30°
∵D为点B关于直线AC的对称点
∴CB=CD,∠BCG=2∠BAC=2∠DCA=60°
∵BE=EF,∠BEF=40°
∴∠EBF=∠EFB=![]() (180°-∠BEF)=70°
(180°-∠BEF)=70°
∠EBC=180°-∠BEC-∠BCE=100°
∴∠CBG=∠EBC-∠EBF=30°
∴∠BGC=180°-∠CBG-∠BCG=90°
∴BG⊥CD,CG=![]() BC=
BC=![]() CD
CD
∴G为CD的中点
∴BG垂直平分CD
∴DF=CF.


科目:初中数学 来源: 题型:
【题目】已知,如图,∠B=∠C=90 ,M是BC的中点,DM平分∠ADC.

(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;
(2)线段DM与AM有怎样的位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
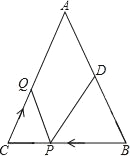
【题目】如图,在△ABC中,∠B=∠C,AB=8,BC=6,点D为AB的中点,点P在线段BC上以每秒2个单位的速度由点B向点C运动,同时点Q在线段CA上以每秒a个单位的速度由点C向点A运动,设运动时间为t(秒)(0≤t≤3).
(1)用含t的代数式表示线段PC的长;
(2)若点P、Q的运动速度相等,t=1时,△BPD与△CQP是否全等,请说明理由.
(3)若点P、Q的运动速度不相等,△BPD与△CQP全等时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ABC=30°,BD平分∠ABC交AC于点D,BC的垂直平分线EF交BC于点E,交BD于点F,若BF=6,则AC的长为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,AD为中线,点P是AD上一点,点Q是AC上一点,且∠BPQ+∠BAQ=180°.
(1)若∠ABP=α,求∠PQC的度数(用含α的式子表示);
(2)求证:BP=PQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走一段距离时到点D处,侧得∠BDF=65°.若直线AB与EF之间的距离为60米.
(1)设池塘两端的距离AB=x米,试用含x的代数式表示CD的长;
(2)当CD=100米时,求A、B两点的距离(计算结果精确到个位).(参考数据:sin45°≈0.71,cos65°≈0.42,tan65°≈2.14.)

查看答案和解析>>
科目:初中数学 来源: 题型:
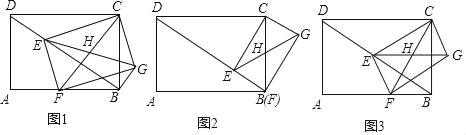
【题目】如图1,矩形ABCD中,AB=8,AD=6;点E是对角线BD上一动点,连接CE,作EF⊥CE交AB边于点F,以CE和EF为邻边作矩形CEFG,作其对角线相交于点H.
(1)①如图2,当点F与点B重合时,CE= ,CG= ;
②如图3,当点E是BD中点时,CE= ,CG= ;
(2)在图1,连接BG,当矩形CEFG随着点E的运动而变化时,猜想△EBG的形状?并加以证明;
(3)在图1,![]() 的值是否会发生改变?若不变,求出它的值;若改变,说明理由;
的值是否会发生改变?若不变,求出它的值;若改变,说明理由;
(4)在图1,设DE的长为x,矩形CEFG的面积为S,试求S关于x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EG是⊙O的切线;
(2)若tanC=![]() ,AC=8,求⊙O的半径.
,AC=8,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE.
求证:△ABC≌△ADE;(填空)
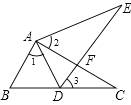
证明:∵∠2+∠E+∠AFE=180° ( )
∠3+∠C+∠CFD=180°(同理)
又∵∠2=∠3( )
∠AFE=∠CFD( )
∴∠E=_________.
∵∠1=∠2(已知)
∴∠1+∠CAD=∠2+∠_______.
即∠BAC=∠DAE
在△ABC和△ADE中
∴△ABC≌△ADE( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com