
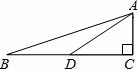
如图所示,在△ABC中,∠C=90°,AD是BC边上的中线,BD=4,AD=2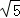 ,则tan∠CAD的值是( )
,则tan∠CAD的值是( )
A. 2 B. 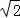 C.
C.  D.
D. 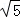
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
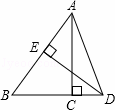
如图,在Rt△ABC中,∠ACB=90°,BC=3,AC= ,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
A. 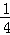 B.
B. 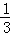 C.
C.  D.
D. 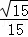
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法①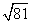 的算术平方根是9 ,②将8450亿元用科学记数法表示为8.45×1011元 ,③
的算术平方根是9 ,②将8450亿元用科学记数法表示为8.45×1011元 ,③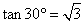 ,④正八边形中心角是
,④正八边形中心角是 45°,⑤若一次函数
45°,⑤若一次函数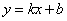 的图象不经过第三象限,则
的图象不经过第三象限,则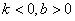 ,其中正确的有( )
,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,足球上守门员在O处开出一高球.球从离地面1米的A处飞出(A在y轴上),把球看成点.其运行的高度y(单位:m)与运行的水平距离x(单位:m)满足关系式y=a(x﹣6)2+h.
(1)①当此球开出后.飞行的最高点距离地面4米时.求y与x满足的关系式.
②在①的情况下,足球落地点C距守门员多少米?(取4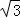 ≈7)
≈7)
③如图所示,若在①的情况下,求落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.求:站在距O带你6米的B处的球员甲要抢到第二个落点D处的求.他应再向前跑多少米?(取2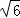 =5)
=5)
(2)球员乙升高为1.75米.在距O点11米的H处.试图原地跃起用头拦截.守门员调整开球高度.若保证足球下落至H正上方时低于球员乙的身高.同时落地点在距O点15米之内.求h的取值范围.
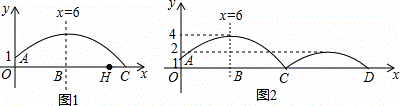
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com