
分析 首先根据(x-3)2$+|y+\frac{1}{3}|$=0,可得x-3=0,|y$+\frac{1}{3}$|=0,据此分别求出x、y的值各是多少;然后化简3x2y-[2xy2-2(xy-$\frac{3}{2}{x}^{2}y$)+3xy]+5xy2,再把求出的x、y的值代入化简后的算式,求出3x2y-[2xy2-2(xy-$\frac{3}{2}{x}^{2}y$)+3xy]+5xy2的值是多少即可.
解答 解:∵(x-3)2$+|y+\frac{1}{3}|$=0,
∴x-3=0,|y$+\frac{1}{3}$|=0,
解得x=3,y=-$\frac{1}{3}$;
3x2y-[2xy2-2(xy-$\frac{3}{2}{x}^{2}y$)+3xy]+5xy2
=3x2y-2xy2+2xy-2×$\frac{3}{2}{x}^{2}y$-3xy+5xy2
=3x2y-2xy2+2xy-3x2y-3xy+5xy2
=3xy2-xy
=3×3×${(-\frac{1}{3})}^{2}$-3×(-$\frac{1}{3}$)
=1+1
=2
∴3x2y-[2xy2-2(xy-$\frac{3}{2}{x}^{2}y$)+3xy]+5xy2的值是2.
点评 (1)此题主要考查了整式的加减-化简求值,要熟练掌握,注意先化简,再求值.
(2)此题还考查了绝对值的非负性质的应用,以及偶次方的非负性质的应用,要熟练掌握,解答此题的关键是分别求出x、y的值各是多少.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:选择题
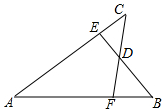 如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )| A. | ① | B. | ② | C. | ①和② | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
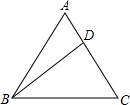 如图,在△ABC中,AB=AC=10,BC=12,有一点D在AC上移动,则AD+BD+CD的最小值是( )
如图,在△ABC中,AB=AC=10,BC=12,有一点D在AC上移动,则AD+BD+CD的最小值是( )| A. | 18 | B. | 18.6 | C. | 20 | D. | 19.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:
如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:| A. | ①②④ | B. | ③④ | C. | ①③④ | D. | ①② |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com