
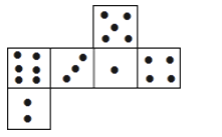
【题目】如图是一个正方体骰子的表面展开图,请根据要求回答问题:
(1)如果1点在上面,3点在左面,几点在前面?
(2)如果5点在下面,几点在上面?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
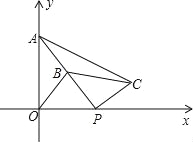
【题目】如图,在平面直角坐标系中,点A的坐标为(0,2),点P(t,0)在x轴上,B是线段PA的中点.将线段PB绕着点P顺时针方向旋转90°,得到线段PC,连结OB、BC.
(1)判断△PBC的形状,并简要说明理由;
(2)当t>0时,试问:以P、O、B、C为顶点的四边形能否为平行四边形?若能,求出相应的t的值?若不能,请说明理由;
(3)当t为何值时,△AOP与△APC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
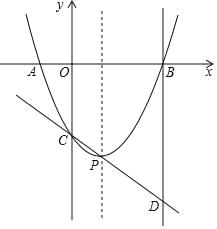
【题目】如图,二次函数 y=ax2﹣2ax+c(a>0)的图象与 x 轴的负半轴和正半轴分别交于 A、B 两点,与 y 轴交于点 C,它的顶点为 P,直线 CP 与过点B 且垂直于 x 轴的直线交于点 D,且 CP:PD=1:2,tan∠PDB=![]() .
.
(1)则 A、B 两点的坐标分别为 A( , ); B( , );
(2)求这个二次函数的解析式;
(3)在抛物线的对称轴上找一点M 使|MC﹣MB|的值最大,则点M 的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
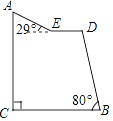
【题目】“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)
查看答案和解析>>
科目:初中数学 来源: 题型:
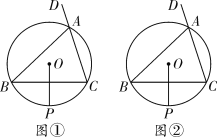
【题目】如图,△ABC是⊙O的内接三角形,∠BAD是它的一个外角,OP⊥BC交⊙O于点P,仅用无刻度的直尺按下列要求分别画图.(保留作图痕迹,不写作法)
(1)在图①中,画出△ABC的角平分线AF;
(2)在图②中,画出△ABC的外角∠BAD的角平分线AG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
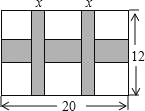
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为△ABC的内心,延长AP交△ABC的外接圆⊙O于D,过D作DE∥BC,交AC的延长线于E点.①则直线DE与⊙O的位置关系是_____;②若AB=4,AD=6,CE=3,则DE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】韦达定理:若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1、x2 , 则x1+x2=﹣![]() , x1x2=
, x1x2=![]() , 阅读下面应用韦达定理的过程:
, 阅读下面应用韦达定理的过程:
若一元二次方程﹣2x2+4x+1=0的两根分别为x1、x2 , 求x12+x22的值.
解:该一元二次方程的△=b2﹣4ac=42﹣4×(﹣2)×1=24>0
由韦达定理可得,x1+x2=﹣![]() =﹣
=﹣![]() =2,x1x2=
=2,x1x2=![]() =
=![]() =﹣
=﹣![]()
x12+x22=(x1+x2)2﹣2x1x2
=22﹣2×(﹣![]() )
)
=5
然后解答下列问题:
(1)设一元二次方程2x2+3x﹣1=0的两根分别为x1,x2, 不解方程,求x12+x22的值;
(2)若关于x的一元二次方程(k﹣1)x2+(k2﹣1)x+(k﹣1)2=0的两根分别为α,β,且α2+β2=4,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△CDB≌△BAG.
(2)如果四边形BFDE是菱形,那么四边形AGBD是什么特殊四边形?并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com