
分析 根据平方差公式将每一个括号展开,然后利用分数的基本性质进行化简.
解答 解:原式=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)(1-$\frac{1}{4}$)(1+$\frac{1}{4}$)…(1-$\frac{1}{n}$)(1+$\frac{1}{n}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…$\frac{n-1}{n}$×$\frac{n+1}{n}$
=$\frac{1}{2}$×$\frac{n+1}{n}$
=$\frac{n+1}{2n}$
点评 本题考查平方差公式的应用,解题的关键是将各个括号利用平方差公式进行分解,本题属于中等题型.


科目:初中数学 来源: 题型:选择题
| A. | x+2>y+2 | B. | -2x<-2y | C. | 1-x>1-y | D. | $\frac{x}{2}>\frac{y}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
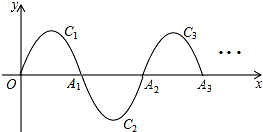 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
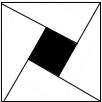 如图,利用四个全等的直角三角形拼成的“赵爽弦图”中,小正方形的面积是1,大正方形的面积是25,直角三角形中较大的锐角为β,那么tanβ=$\frac{4}{3}$.
如图,利用四个全等的直角三角形拼成的“赵爽弦图”中,小正方形的面积是1,大正方形的面积是25,直角三角形中较大的锐角为β,那么tanβ=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
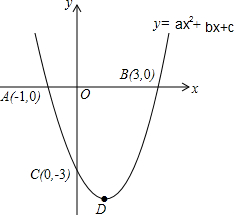 已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B和点C的坐标分别为(3,0)(0,-3),抛物线的对称轴为x=1,D为抛物线 的顶点.
已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B和点C的坐标分别为(3,0)(0,-3),抛物线的对称轴为x=1,D为抛物线 的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 边AC的垂直平分线上 | B. | 边AB的垂直平分线上 | ||
| C. | 边BC的垂直平分线上 | D. | 边AC的高上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com