
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | y | |
| 正方形纸板(张) | x | 2y |
| 长方形纸板(张) | 4x | 3y |
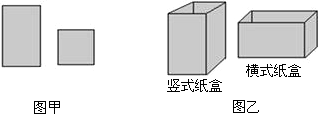
分析 (1)①可根据每个竖式纸盒需1个正方形纸板和4个长方形纸板,每个横式纸盒需3个长方形纸板和2个正方形纸板来填空.
②生产竖式纸盒用的正方形纸板+生产横式纸盒用的正方形纸板=150张;生产竖式纸盒用的长方形纸板+生产横式纸盒用的长方形纸板=300张.由此得出符合条件的方案.
(2)设做竖式纸盒x个,横式纸盒y个,列出含有a的二元一次方程组,解方程组得出y关于a的等式,根据题中给出的a的取值范围便可求出y的取值范围,进而求出a的值.
解答 解:(1)①如表:
| 纸盒 纸板 | 竖式纸盒(个) | 横式纸盒(个) |
| x | y | |
| 正方形纸板(张) | x | 2y |
| 长方形纸板(张) | 4x | 3y |
点评 本题主要考查了二元一次方程组和一元一次不等式组的实际应用,解题关键是弄清题意,合适的等量关系,列出方程组,属于中档题.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y2<y3<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
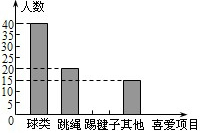 某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查,整理收集到的数据,绘制成如图所示的统计图.若该校共有1000名学生,估计喜欢“踢毽子”的学生有250人.
某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查,整理收集到的数据,绘制成如图所示的统计图.若该校共有1000名学生,估计喜欢“踢毽子”的学生有250人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
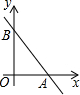 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,点P(m,0)为x轴上一点.
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,点P(m,0)为x轴上一点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
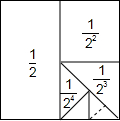 在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.
在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
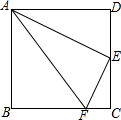 如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.
如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com