
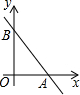 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,点P(m,0)为x轴上一点.
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,点P(m,0)为x轴上一点.分析 (1)先求得直线l与x、y轴的交点,然后根据待定系数法即可求解;
(2)根据三角形面积求得PA的长,进而即可求得P的坐标;
(3)根据题意得出△PAB是以AB为腰的等腰三角形,根据等腰三角形的性质即可求得.
解答 解:(1)∵直线l:y=-$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,
∴A(3,0),B(0,4),
∵P(-1,0),
设直线BP的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{b=4}\\{-k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=4}\\{b=4}\end{array}\right.$.
∴直线BP的解析式为y=4x+4;
(2)∵S△PAB=$\frac{1}{2}$PA•OB=12,
∴$\frac{1}{2}$PA×4=12,
∴PA=6,
∵A(3,0),
∴P(9,0)或(-3,0);
(3)∵A(3,0),B(0,4),
∴OA=3,OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
要使以P、A、B三点组成的图形为轴对称图形,且m≥0,
则△PAB是以AB为腰的等腰三角形,
∴P(8,0).
点评 本题是一次函数的综合题,考查了待定系数法求一次函数的解析式,三角形的面积以及等腰三角形的性质等.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 边数越多的多边形,它的内角和也越大 | |
| B. | 多边形随着边数的增加,它的外角和和随着增加 | |
| C. | 当多边形的边数扩大两倍时,多边形的内角和也扩大两倍 | |
| D. | 当边数超过4时,多边形的内角一定大于相邻的外角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
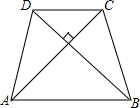 如图,等腰梯形ABCD的面积为100cm2,AC⊥BD.
如图,等腰梯形ABCD的面积为100cm2,AC⊥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
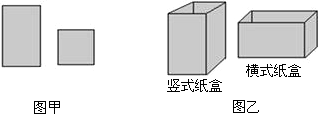
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | y | |
| 正方形纸板(张) | x | 2y |
| 长方形纸板(张) | 4x | 3y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
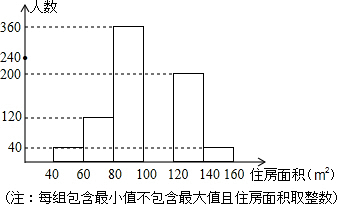 2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:
2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:| 年收入(万元) | 3.2 | 3.8 | 5.0 | 7.0 | 12.0 |
| 被调查的消费者数(人) | 200 | 500 | 200 | 70 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com