
(本题满分12分)
如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D.
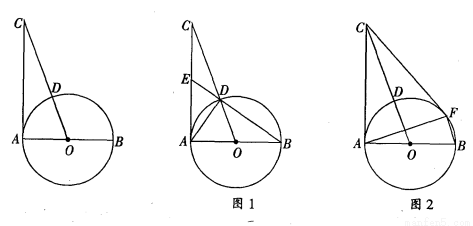
(1)如图1,连接BD并延长BD交AC于点E,连接AD.
①证明:△CDE∽△CAD;
②若AB=2,AC=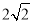 .求CD和CE的长;
.求CD和CE的长;
(2)如图2,过点C作⊙O的另一条切线,切点为F,连结AF、BF,若OC=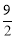 BF,求
BF,求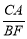 的值.
的值.
(1)①证明见试题解析;②CD=2,CE=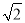 ;(2)
;(2)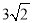 .
.
【解析】
试题分析:(1)由AC是⊙O的切线,得到∠1+∠BAD=90°,又由AB是⊙O的直径,得到∠B+∠BAD=90°,故有∠1=∠B,又由OB=OD,得到∠2=∠B,又因∠2=∠3,得到∠3=∠B,得到∠1=∠3,由∠C=∠C,得到△CDE∽△CAD;
(2)在Rt△AOC中,算出OC,进而算出CD的长,由△CDE∽△CAD,得到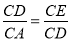 ,解出CE的长;
,解出CE的长;
(3)由△ABF∽△COA,得到 ,故
,故 ,又OC=
,又OC= BF,AB=2r,OA=r,得到
BF,AB=2r,OA=r,得到 ,得到BF=
,得到BF=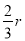 ,OC=3r,在Rt△COA中,由勾股定理求出CA的长,再算
,OC=3r,在Rt△COA中,由勾股定理求出CA的长,再算 .
.
试题解析:(1)证明:∵AC是⊙O的切线,∴∠1+∠BAD=90°,又∵AB是⊙O的直径,∴∠B+∠BAD=90°,∴∠1=∠B,又∵OB=OD,∴∠2=∠B,又∵∠2=∠3,∴∠3=∠B,∴∠1=∠3,∵∠C=∠C,∴△CDE∽△CAD;
(2)在Rt△AOC中,OC=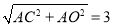 ,∴CD=OC-OD=3-1=2,∵△CDE∽△CAD,∴
,∴CD=OC-OD=3-1=2,∵△CDE∽△CAD,∴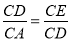 ,即
,即 ,∴CE=
,∴CE=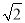 ;
;
(3)由△ABF∽△COA,∴ ,∴
,∴ ,又OC=
,又OC= BF,AB=2r,OA=r(r为⊙O的半径),∴
BF,AB=2r,OA=r(r为⊙O的半径),∴ ,∴BF=
,∴BF=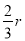 ,OC=3r,在Rt△COA中,由勾股定理知:CA=
,OC=3r,在Rt△COA中,由勾股定理知:CA=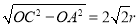 ,∴
,∴ .
.
考点:圆的综合题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:2014-2015学年福建省南平市水东学校七年级上学期期中考试数学试卷(解析版) 题型:解答题
(6分)一只小虫从某点P出发,在一条直线上来回爬行,若把向右爬行的路程记为正数,向左爬行的路程记为负数,则爬行各段路程(单位:厘米)依次为:+5,-3,+10,-8,-6,+12,-10.
(1)、通过计算说明小虫是否回到起点P.
(2)、如果小虫爬行的速度为0.5厘米/秒,那么小虫共爬行了多长时间.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省诸城市九年级下学期开学检测数学试卷(解析版) 题型:选择题
把4个正方体摆放成如图所示的几何体,该几何体的俯视图是( )
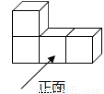
A. B.
B.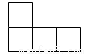 C.
C.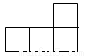 D.
D.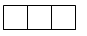
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级12月学情监测数学试卷(解析版) 题型:选择题
如图,在△ABC中,∠BAC=90°,AD⊥BC与D,DE⊥AB与E,若AD=3,DE=2,则AC=( )

A.
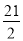 B.
B. C.
C.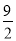 D.
D.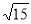
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级12月学情监测数学试卷(解析版) 题型:选择题
已知反比例函数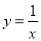 ,下列结论中不正确的是( )
,下列结论中不正确的是( )
A.图象经过点(-1,-1) B.图象在第一、三象限
C.当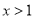 时,
时,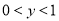 D.当
D.当 时,y随着x的增大而增大
时,y随着x的增大而增大
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,△ABC内接于⊙O,AO=2,BC= ,则∠BAC的度数为 °.
,则∠BAC的度数为 °.
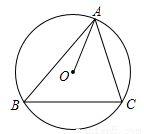
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期末联考数学试卷(解析版) 题型:解答题
在一个口袋中有4个完全相同的小球,把它们分别标上数字﹣1,0,1,2,随机的摸出一个小球记录数字然后放回,再随机的摸出一个小球记录数字.用树状图或列表法求下列事件的概率:(1)、两次都是正数的概率;(2)、两次的数字和等于0的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com