
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 上一动点,过三点
上一动点,过三点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
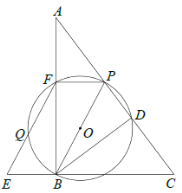
(1)求证:四边形![]() 为平行四边形.
为平行四边形.
(2)当![]() 时,求
时,求![]() 的长.
的长.
(3)在点![]() 整个运动过程中,
整个运动过程中,
①当![]() 中满足某两条线段相等,求所有满足条件的
中满足某两条线段相等,求所有满足条件的![]() 的长.
的长.
②当点![]() 三点共线时,
三点共线时,![]() 交
交![]() 于点
于点![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值. (请直接写出答案)
的值. (请直接写出答案)
【答案】(1)见解析;(2)PD=![]() ;(3)①
;(3)①![]() 或
或![]() 或PF=
或PF=![]() ;②
;②![]()
【解析】
(1)证明两组对边分别平行即可证明四边形FEBP为平行四边形;
(2)①由AC=10,sinC=![]() ,可得BC=6,AB=8,sinA=
,可得BC=6,AB=8,sinA=![]() ,所以AD=ABsin∠ABD=ABsin∠C=8×
,所以AD=ABsin∠ABD=ABsin∠C=8×![]() =
=![]() ,再求得AP=
,再求得AP=![]() ,最后PD=AD﹣AP解答即可;
,最后PD=AD﹣AP解答即可;
②分三种情况讨论:Ⅰ.当PF=PD时,Ⅱ.当QF=PD时,Ⅲ.当QF=PF时,分别解答即可;
③连接FD,求出FD的长,再利用勾股定理求出QF的长.
(1)证明:
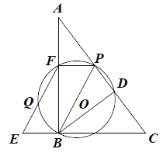
∵![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() ,∴
,∴![]() .
.
又∵![]() ,
,
所以四边形![]() 是平行四边形.
是平行四边形.
(2)在![]() 中,∵
中,∵![]() ,
,
∴![]() .
.
∵![]() ,
,
![]() ,
, ![]() .
.
∴![]()
(3)设![]() ,则
,则![]() ,
,
①当![]() 时,如图.
时,如图.
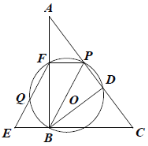
![]()
∴![]()
∴![]() ,
,
∴![]() .
.
②当![]() 时,如图,连结
时,如图,连结![]() .
.
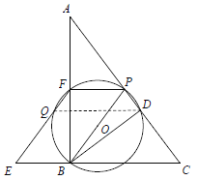
∴![]() ,即
,即![]()
∴![]() ,所以
,所以![]() .
.
由(1)得:四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
在![]() 中,易得
中,易得![]()
∴![]() ,
,
则![]() ,
,
∴![]() .
.
③当![]() 时,如图,连结
时,如图,连结![]() .
.

∵![]()
∴![]() ,
,
∴![]()
在![]() 中,易得
中,易得![]()
∴![]() ,且
,且![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
综上所述,所有满足条件的PF的长有:![]() ;
;
②连接QD,连接FD,交BP于点H.
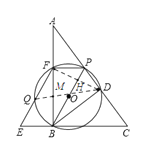
∵Q,O,D三点共线
∴QD为⊙O直径.
∵EF∥BP,O为QD中点,
∴H为DF中点,
∵BP为直径,
∴BP⊥DF,![]() ,
,
∴PF=PD.
设PF=3x,则AF=4x,AP=5x
AD=ABsin∠ABD=ABsin∠C=8×![]() ,
,
∴PD=AD﹣AP=![]() ﹣5x,
﹣5x,
∴3x=![]() ﹣5x,
﹣5x,
∴x=![]() ,PF=PD=
,PF=PD=![]() ,
,
在Rt△ABC中,BD=![]() ,
,
![]()
在Rt△PDB中,DH=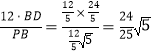 ,
,
∴DF=![]() ,
,
在Rt△DQF中,QF=![]() ,
,
易知△FQM∽△BDM,
∴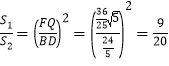 .
.


科目:初中数学 来源: 题型:
【题目】如图![]() ,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”
,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角” ![]() 约为
约为![]() ,而当手指接触键盘时,肘部形成的“手肘角”
,而当手指接触键盘时,肘部形成的“手肘角”![]() 约为
约为![]() .图
.图![]() 是其侧面简化示意图,其中视线
是其侧面简化示意图,其中视线![]() 水平,且与屏幕
水平,且与屏幕![]() 垂直.
垂直.

(![]() )若屏幕上下宽
)若屏幕上下宽![]() ,科学使用电脑时,求眼睛与屏幕的最短距离
,科学使用电脑时,求眼睛与屏幕的最短距离![]() 的长.
的长.
(![]() )若肩膀到水平地面的距离
)若肩膀到水平地面的距离![]() ,上臂
,上臂![]() ,下臂
,下臂![]() 水平放置在键盘上,其到地面的距离
水平放置在键盘上,其到地面的距离![]() ,请判断此时
,请判断此时![]() 是否符合科学要求的
是否符合科学要求的![]() ?
?
(参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).
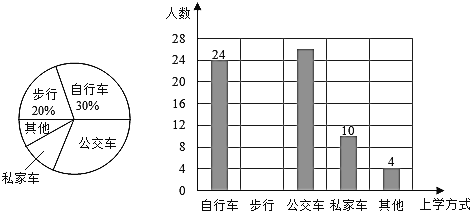
(1)这次调查中,一共抽取了_____名学生;
(2)补全条形统计图;
(3)估计全校所有学生中有多少人乘坐公交车上学?
(4)小明在上学的路上要经过2个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到信号灯是相互独立的.求小明在上学路上到第二个路口时第一次遇到红灯的概率(请用“画树状图”或“列表”的方法写出分析过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
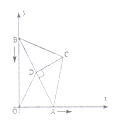
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的高,点
边的高,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 在第一象限,若
在第一象限,若![]() 从原点出发,沿
从原点出发,沿![]() 轴向右以每秒1个单位长的速度运动,则点
轴向右以每秒1个单位长的速度运动,则点![]() 随之沿
随之沿![]() 轴下滑,并带动
轴下滑,并带动![]() 在平面内滑动,设运动时间为
在平面内滑动,设运动时间为![]() 秒,当
秒,当![]() 到达原点时停止运动
到达原点时停止运动
(1)连接![]() ,线段
,线段![]() 的长随
的长随![]() 的变化而变化,当
的变化而变化,当![]() 最大时,
最大时,![]() ______.
______.
(2)当![]() 的边与坐标轴平行时,
的边与坐标轴平行时,![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
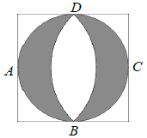
【题目】文艺复兴时期,意大利艺术大师达芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为![]() ,
,![]() 所在圆的圆心为点
所在圆的圆心为点![]() (或
(或![]() ). 若正方形的边长为2,则图中阴影部分的面积为( )
). 若正方形的边长为2,则图中阴影部分的面积为( )
A. ![]() B. 2C.
B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
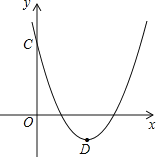
(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com