
【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).
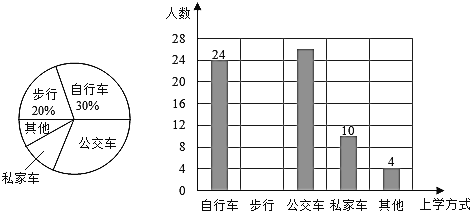
(1)这次调查中,一共抽取了_____名学生;
(2)补全条形统计图;
(3)估计全校所有学生中有多少人乘坐公交车上学?
(4)小明在上学的路上要经过2个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到信号灯是相互独立的.求小明在上学路上到第二个路口时第一次遇到红灯的概率(请用“画树状图”或“列表”的方法写出分析过程).
【答案】(1)80;(2)见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据上学方式为“自行车”的学生数除以所占的百分比即可求出调查的学生总数;(2)总人数乘以“步行”的学生所占的百分比求出“步行”的学生人数,补全统计图即可;(3)总人数减去其它四种方式的人数求出上学方式为“公交车”的学生的人数,除以抽查的总人数求出上学方式为“公交车”的学生所占百分比,乘以2400即可得到结果;(4)根据题意画出相应的树状图,得出所有等可能的情况数,找出到第二个路口时第一次遇到红灯的情况数,根据概率公式即可得答案.
(1)24÷30%=80(名);
故答案为:80
(2)被抽到的学生中,步行的人数为![]() ,
,
条形统计图如下:
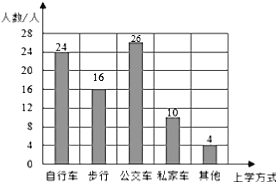
(3)被抽到的学生中,乘公交车的人数为![]() ,
,
∴全校所有学生中乘坐公交车上学的人数约为![]()
(4).画树状图如下:
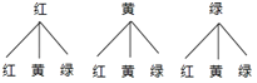
由树状图知,共有9种等可能结果,其中到第二个路口时第一次遇到红灯的结果数为2,所以到第二个路口时第一次遇到红灯的概率为![]()


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
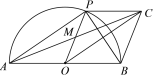
【题目】如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的动点,PC∥AB,点M是OP中点.
(1)求证:四边形AOCP是平行四边形;
(2)填空:①当∠ABP= 时,四边形AOCP是菱形;
②连接BP,当∠ABP= 时,PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() AD的长为半径作弧,两弧交于点M、N;第二步,过M、N两点作直线分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=8,AF=6,CD=4,则BE的长是( )
AD的长为半径作弧,两弧交于点M、N;第二步,过M、N两点作直线分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=8,AF=6,CD=4,则BE的长是( )

A. 12B. 11C. 13D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
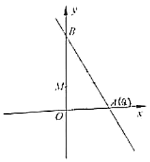
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上,把
上,把![]() 沿着直线
沿着直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,联结
处,联结![]() ,如果直线
,如果直线![]() 与直线
与直线![]() 所构成的夹角为60°,那么点
所构成的夹角为60°,那么点![]() 的坐标是____________
的坐标是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
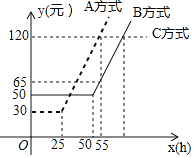
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
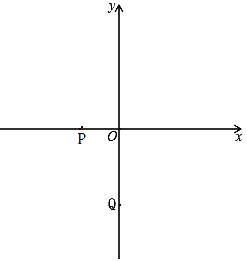
【题目】如图,已知:P(-1,0),Q(0,-2).
(1)求直线PQ的函数解析式;
(2)如果M(0,![]() )是线段OQ上一动点,抛物线
)是线段OQ上一动点,抛物线![]() 经过点M和点P,
经过点M和点P,
①求抛物线![]() 与
与![]() 轴另一交点N的坐标(用含
轴另一交点N的坐标(用含![]() ,
,![]() 的代数式表示);
的代数式表示);
②若PN=![]() 是,抛物线
是,抛物线![]() 有最大值
有最大值![]() +1,求此时
+1,求此时![]() 的值;
的值;
③若抛物线![]() 与直线PQ始终都有两个公共点,求
与直线PQ始终都有两个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 上一动点,过三点
上一动点,过三点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
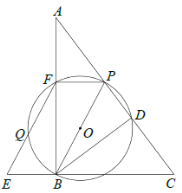
(1)求证:四边形![]() 为平行四边形.
为平行四边形.
(2)当![]() 时,求
时,求![]() 的长.
的长.
(3)在点![]() 整个运动过程中,
整个运动过程中,
①当![]() 中满足某两条线段相等,求所有满足条件的
中满足某两条线段相等,求所有满足条件的![]() 的长.
的长.
②当点![]() 三点共线时,
三点共线时,![]() 交
交![]() 于点
于点![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值. (请直接写出答案)
的值. (请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是40元,根据市场调查:在一段时间内,销售单价是50元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>50),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) | ① |
销售玩具获得利润ω(元) | ② |
(2)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于54元,且商场要完成不少于400件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com