
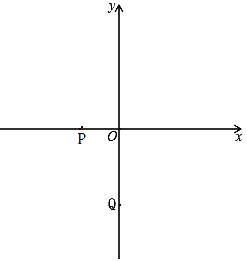
【题目】如图,已知:P(-1,0),Q(0,-2).
(1)求直线PQ的函数解析式;
(2)如果M(0,![]() )是线段OQ上一动点,抛物线
)是线段OQ上一动点,抛物线![]() 经过点M和点P,
经过点M和点P,
①求抛物线![]() 与
与![]() 轴另一交点N的坐标(用含
轴另一交点N的坐标(用含![]() ,
,![]() 的代数式表示);
的代数式表示);
②若PN=![]() 是,抛物线
是,抛物线![]() 有最大值
有最大值![]() +1,求此时
+1,求此时![]() 的值;
的值;
③若抛物线![]() 与直线PQ始终都有两个公共点,求
与直线PQ始终都有两个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①N(
;(2)①N(![]() ,0);②
,0);②![]() 或
或![]() ;③详见解析.
;③详见解析.
【解析】
(1)利用待定系数法求一次函数关系式即可;
(2) ①由抛物线![]() 经过点M和点P可把点M和点P代入,再利用因式分解法变形可求得结果;
经过点M和点P可把点M和点P代入,再利用因式分解法变形可求得结果;
②![]() 分两种情况,一种点N在点P的左侧,另一种在右侧,分别代入可求出;
分两种情况,一种点N在点P的左侧,另一种在右侧,分别代入可求出;
③联立抛物线解析式和直线PQ的解析式,得到关于x的方程,根据“始终都有两个公共点”得![]() >0,求出a的范围.
>0,求出a的范围.
解:(1)设直线PQ的函数解析式为y=kx+b,把P(-1,0),Q(0,-2)代入得
![]() ,解得
,解得![]() ,
,
∴![]() ,
,

(2)①y=ax2+bx+ c 过M(0,m)和P(-1,0),
则![]() 过P(-1,0)
过P(-1,0)
∴![]() ,
,![]()
∴![]()
∴![]()
∴N(![]() ,0)
,0)
②M(0,m),![]() ,抛物线y=ax2+bx+c有最大值
,抛物线y=ax2+bx+c有最大值![]() ,
,
(![]() ,
,![]() )
)
![]()
当![]() 时,分两种情况,
时,分两种情况,
(I)![]()
![]()
解得:![]() ,
,![]() (经验证,均成立)
(经验证,均成立)
(II)![]()
![]() ,解得:
,解得:![]() ,
,![]() (经验证,均成立)
(经验证,均成立)
∴![]() 或
或![]()
③![]()
得![]() ,
,
![]()
![]()
∵![]() ,
,
![]()
∴当![]() 或
或![]() 时,
时,![]() 始终为正,
始终为正,
即抛物线y=ax2+bx+c与直线PQ始终都有两个公共点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
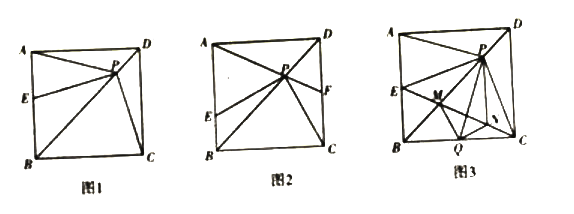
【题目】如图1,在正方形ABCD中,AD=6,点P是对角线BD上任意一点,连接PA,PC,过点P作PE⊥PC交直线AB于点E.
(1)求证: PC=PE;
(2)延长AP交直线CD于点F.
①如图2,若点F是CD的中点,求△APE的面积;
②若△APE的面积是![]() ,则DF的长为_________;
,则DF的长为_________;
(3)如图3,点E在边AB上,连接EC交BD于点M,作点E关于BD的对称点Q,连接PQ, MQ,过点P作![]() 交EC于点N,连接
交EC于点N,连接![]() ,若
,若![]() ,则
,则![]() 的面积是________.
的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水产经销商以10元/千克的价格收购了1000千克的鳊鱼围养在湖塘中(假设围养期每条鳊鱼的重量保持不变),据市场推测,经过湖塘围养后的鳊鱼的市场价格每围养一天能上涨1元/千克,在围养过程中(最多围养20天),平均每围养一天有10千克的鳊鱼会缺氧浮水。假设对缺氧浮水的鳊鱼能以5元/千克的价格抛售完.
(1)若围养x天后,该水产经销商将活着的鳊鱼一次性出售,加上抛售的缺氧浮水鳊鱼,能获利8500元,则需要围养多少天?
(2)若围养期内,每围养一天需支出各种费用450元,则该水产经销商最多可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).
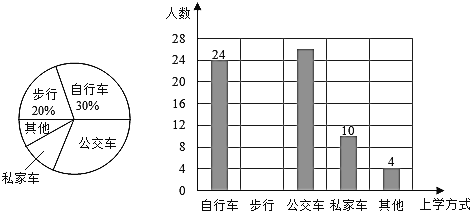
(1)这次调查中,一共抽取了_____名学生;
(2)补全条形统计图;
(3)估计全校所有学生中有多少人乘坐公交车上学?
(4)小明在上学的路上要经过2个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到信号灯是相互独立的.求小明在上学路上到第二个路口时第一次遇到红灯的概率(请用“画树状图”或“列表”的方法写出分析过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的高,点
边的高,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 在第一象限,若
在第一象限,若![]() 从原点出发,沿
从原点出发,沿![]() 轴向右以每秒1个单位长的速度运动,则点
轴向右以每秒1个单位长的速度运动,则点![]() 随之沿
随之沿![]() 轴下滑,并带动
轴下滑,并带动![]() 在平面内滑动,设运动时间为
在平面内滑动,设运动时间为![]() 秒,当
秒,当![]() 到达原点时停止运动
到达原点时停止运动
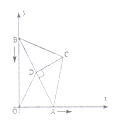
(1)连接![]() ,线段
,线段![]() 的长随
的长随![]() 的变化而变化,当
的变化而变化,当![]() 最大时,
最大时,![]() ______.
______.
(2)当![]() 的边与坐标轴平行时,
的边与坐标轴平行时,![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文艺复兴时期,意大利艺术大师达芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为![]() ,
,![]() 所在圆的圆心为点
所在圆的圆心为点![]() (或
(或![]() ). 若正方形的边长为2,则图中阴影部分的面积为( )
). 若正方形的边长为2,则图中阴影部分的面积为( )
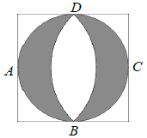
A. ![]() B. 2C.
B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() . 将线段
. 将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,
,![]() 是边
是边![]() 上的一动点,连接
上的一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)点![]() 在边
在边![]() 上,且
上,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
①判断![]() 与
与![]() 的位置关系,并证明你的结论;②连接
的位置关系,并证明你的结论;②连接![]() ,若
,若![]() ,请直接写出线段
,请直接写出线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com