
【题目】水产经销商以10元/千克的价格收购了1000千克的鳊鱼围养在湖塘中(假设围养期每条鳊鱼的重量保持不变),据市场推测,经过湖塘围养后的鳊鱼的市场价格每围养一天能上涨1元/千克,在围养过程中(最多围养20天),平均每围养一天有10千克的鳊鱼会缺氧浮水。假设对缺氧浮水的鳊鱼能以5元/千克的价格抛售完.
(1)若围养x天后,该水产经销商将活着的鳊鱼一次性出售,加上抛售的缺氧浮水鳊鱼,能获利8500元,则需要围养多少天?
(2)若围养期内,每围养一天需支出各种费用450元,则该水产经销商最多可获利多少元?
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】某文具店经销甲、乙两种不同的笔记本.已知:两种笔记本的进价之和为10元,甲种笔记本每本获利2元,乙种笔记本每本获利1元,马阳光同学买4本甲种笔记本和3本乙种笔记本共用了47元.
(1)甲、乙两种笔记本的进价分别是多少元?
(2)该文具店购入这两种笔记本共60本,花费不超过296元,则购买甲种笔记本多少本时该文具店获利最大?
(3)店主经统计发现平均每天可售出甲种笔记本350本和乙种笔记本150本.如果甲种笔记本的售价每提高1元,则每天将少售出50本甲种笔记本;如果乙种笔记本的售价每提高1元,则每天少售出40本乙种笔记本,为使每天获取的利润更多,店主决定把两种笔记本的价格都提高![]() 元,在不考虑其他因素的条件下,当
元,在不考虑其他因素的条件下,当![]() 定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是【 】

A.AE=6cm B.![]()
C.当0<t≤10时,![]() D.当t=12s时,△PBQ是等腰三角形
D.当t=12s时,△PBQ是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() AD的长为半径作弧,两弧交于点M、N;第二步,过M、N两点作直线分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=8,AF=6,CD=4,则BE的长是( )
AD的长为半径作弧,两弧交于点M、N;第二步,过M、N两点作直线分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=8,AF=6,CD=4,则BE的长是( )

A. 12B. 11C. 13D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=90°,E是AC的中点,AE=2.经过点E作△ABE外接圆的切线交BC于点D,过点C作CF⊥BC交BE的延长线于点F,连接FD交AC于点H,FD平分∠BFC.
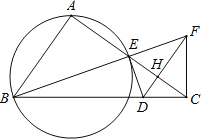
(1)求证:DE=DC;
(2)求证:HE=HC=1;
(3)求BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
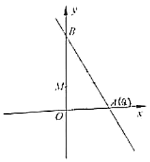
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上,把
上,把![]() 沿着直线
沿着直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,联结
处,联结![]() ,如果直线
,如果直线![]() 与直线
与直线![]() 所构成的夹角为60°,那么点
所构成的夹角为60°,那么点![]() 的坐标是____________
的坐标是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
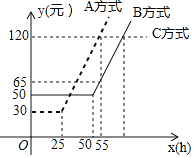
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
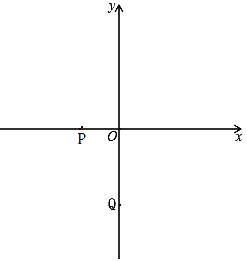
【题目】如图,已知:P(-1,0),Q(0,-2).
(1)求直线PQ的函数解析式;
(2)如果M(0,![]() )是线段OQ上一动点,抛物线
)是线段OQ上一动点,抛物线![]() 经过点M和点P,
经过点M和点P,
①求抛物线![]() 与
与![]() 轴另一交点N的坐标(用含
轴另一交点N的坐标(用含![]() ,
,![]() 的代数式表示);
的代数式表示);
②若PN=![]() 是,抛物线
是,抛物线![]() 有最大值
有最大值![]() +1,求此时
+1,求此时![]() 的值;
的值;
③若抛物线![]() 与直线PQ始终都有两个公共点,求
与直线PQ始终都有两个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com