
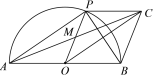
【题目】如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的动点,PC∥AB,点M是OP中点.
(1)求证:四边形AOCP是平行四边形;
(2)填空:①当∠ABP= 时,四边形AOCP是菱形;
②连接BP,当∠ABP= 时,PC是⊙O的切线.
【答案】(1)证明见解析;(2)①30°;②45°.
【解析】
(1)先判断出四边形OBCP是平行四边形,得出OB=PC,OB∥PC,再判断出OA=PC,从而得出结论;
(2)根据圆周角定理得到∠AOP=60°,推出△AOP是等边三角形,得到AP=AO,于是得到四边形AOCP是菱形;由圆周角定理得到∠AOP=90°,根据平行线的性质得到∠OPC=∠AOP=90°,于是得到结论.
(1)∵点M是OP中点,
∴AM=CM,
∵AO=BO,
∴OM∥BC,
∴OP∥BC,
∵PC∥AB,
∴四边形OBCP是平行四边形;
(2)当∠ABP=30度时,四边形AOCP是菱形;
理由:∵∠ABP=30°,
∴∠AOP=60°,
∵AO=PO,
∴△AOP是等边三角形,
∴AP=AO,
∴四边形AOCP是菱形;
当∠ABP=45度时,PC是⊙O的切线;
理由:∵∠ABP=45°,
∴∠AOP=90°,
∵AO∥PC,
∴∠OPC=∠AOP=90°,
∴PC是⊙O的切线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4分别与x轴、y轴交于点A,B,双曲线![]() (k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.
(k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快复工复产,某企业需运输批物资.据调查得知,2辆大货车与3辆小货车一次可以运输600箱;5辆大货车与6辆小货车一次可以运输1350箱.
(1)求1辆大货车和1辆小货车一次可以分别运输多少箱物资;
(2)计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5 000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元,请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(-1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:①二次函数y=ax2+bx+c的最小值为-4a;②若-1≤x2≤4,则0≤y2≤5a;③若y2>y1,则x2>4;④一元二次方程cx2+bx+a=0的两个根为-1和![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
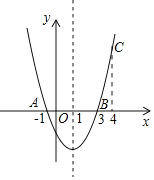
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心,以小于AC的长为半径作弧,分别交AC,AB于点M,N;②分别以点M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点O;③连接AP,交BC于点E.若CE=3,BE=5,则AC的长为( )
MN的长为半径作弧,两弧相交于点O;③连接AP,交BC于点E.若CE=3,BE=5,则AC的长为( )
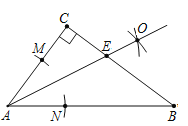
A. 4B. 5C. 6D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=k1x+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y2=![]() 的图象分别交于C,D两点,且D(2,-3),OA=2.
的图象分别交于C,D两点,且D(2,-3),OA=2.
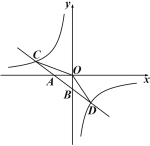
(1)求一次函数与反比例函数的解析式;
(2)请直接写出不等式k1x+b-![]() ≥0的解集;
≥0的解集;
(3)动点P(0,m)在y轴上运动,当|PC-PD|的值最大时,请写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
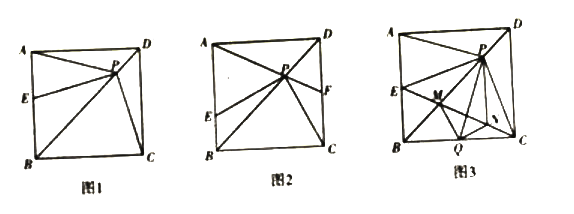
【题目】如图1,在正方形ABCD中,AD=6,点P是对角线BD上任意一点,连接PA,PC,过点P作PE⊥PC交直线AB于点E.
(1)求证: PC=PE;
(2)延长AP交直线CD于点F.
①如图2,若点F是CD的中点,求△APE的面积;
②若△APE的面积是![]() ,则DF的长为_________;
,则DF的长为_________;
(3)如图3,点E在边AB上,连接EC交BD于点M,作点E关于BD的对称点Q,连接PQ, MQ,过点P作![]() 交EC于点N,连接
交EC于点N,连接![]() ,若
,若![]() ,则
,则![]() 的面积是________.
的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”
,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角” ![]() 约为
约为![]() ,而当手指接触键盘时,肘部形成的“手肘角”
,而当手指接触键盘时,肘部形成的“手肘角”![]() 约为
约为![]() .图
.图![]() 是其侧面简化示意图,其中视线
是其侧面简化示意图,其中视线![]() 水平,且与屏幕
水平,且与屏幕![]() 垂直.
垂直.

(![]() )若屏幕上下宽
)若屏幕上下宽![]() ,科学使用电脑时,求眼睛与屏幕的最短距离
,科学使用电脑时,求眼睛与屏幕的最短距离![]() 的长.
的长.
(![]() )若肩膀到水平地面的距离
)若肩膀到水平地面的距离![]() ,上臂
,上臂![]() ,下臂
,下臂![]() 水平放置在键盘上,其到地面的距离
水平放置在键盘上,其到地面的距离![]() ,请判断此时
,请判断此时![]() 是否符合科学要求的
是否符合科学要求的![]() ?
?
(参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).
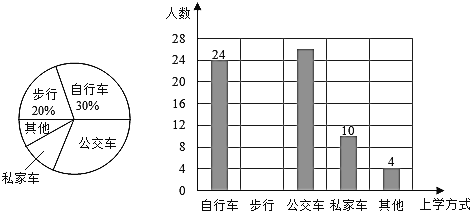
(1)这次调查中,一共抽取了_____名学生;
(2)补全条形统计图;
(3)估计全校所有学生中有多少人乘坐公交车上学?
(4)小明在上学的路上要经过2个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到信号灯是相互独立的.求小明在上学路上到第二个路口时第一次遇到红灯的概率(请用“画树状图”或“列表”的方法写出分析过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com