
分析 由1=$\frac{1}{1}=\frac{2}{2}=\frac{2}{1×2}=2×(1-\frac{1}{2})$,$\frac{1}{1+2}=\frac{1}{3}=\frac{2}{6}=2×(\frac{1}{2}-\frac{1}{3})$,同理可得$\frac{1}{1+2+3}=2×(\frac{1}{3}-\frac{1}{4})$,从而可以求得1+$\frac{1}{1+2}$$+\frac{1}{1+2+3}$$+…+\frac{1}{1+2+3+…+2012}$=2×$(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{2012}-\frac{1}{2013})$=2×$(1-\frac{1}{2013})$,然后去括号,化简即可求得问题的答案.
解答 解:1+$\frac{1}{1+2}$$+\frac{1}{1+2+3}$$+…+\frac{1}{1+2+3+…+2012}$
=$\frac{1}{1}$$+\frac{1}{3}+\frac{1}{6}+…+\frac{1}{1+2+3+…+2012}$
=$\frac{2}{2}+\frac{2}{6}+\frac{2}{12}+…+\frac{2}{2×(1+2+3+…+2012)}$
=2×$(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{2012}-\frac{1}{2013})$
=2×$(1-\frac{1}{2013})$
=2×$\frac{2012}{2013}$
=$\frac{4024}{2013}$.
点评 本题考查有理数的加减混合运算,关键是发现整个式子的规律,进行巧妙变化,从而解答本题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
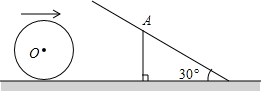 如图,桌面上有一半径为r小球向右滚动,前面有一块与桌面垂直的垂直挡板AC和一块与桌面成30°角B的斜挡板AB,两块挡板相交于点A,且有一端都紧靠桌面,如果AC=2.
如图,桌面上有一半径为r小球向右滚动,前面有一块与桌面垂直的垂直挡板AC和一块与桌面成30°角B的斜挡板AB,两块挡板相交于点A,且有一端都紧靠桌面,如果AC=2. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
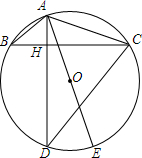 如图,已知AE为⊙O的直径,△ABC内接于⊙O,AD⊥BC于H交⊙O于D.
如图,已知AE为⊙O的直径,△ABC内接于⊙O,AD⊥BC于H交⊙O于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com