
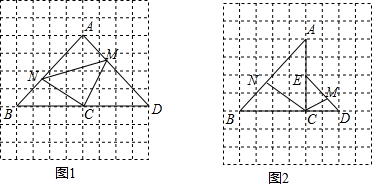
分析 ①先证明△BNC≌△AMC得△NCM是等腰直角三角形,即CM+CN的最小值,就是MN最小值的值,当点M,N分别在线段AD,AB的中点时,MN最小,求出此时的值即可;
②如图3,作辅助线,构建与△ACB全等的△EGH,将CM与CN两条线段利用相等线段,放在同一个三角形EGH中,利用作对称点的方法找到最小值时点M的位置,即PC与DE的交点就是最小值时的点M,根据线段垂直平分线的性质可知:CM+CN=CM+MG=CM+PM=PC,这里要利用△ANC≌△HMG,证明CN=GM,所以CM+CN就是PC的长,利用勾股定理可计算得出.
解答 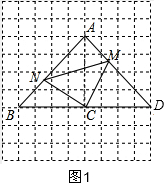 解:①如图1,连接AC,
解:①如图1,连接AC,
∵三角形ACB与ACD是等腰直角三角形,
∴∠B=∠CAM=45°,AC=BC,
在△BNC和△AMC中,
∵$\left\{\begin{array}{l}{BN=AM}\\{∠B=∠CAM}\\{BC=AC}\end{array}\right.$,
∴△BNC≌△AMC(SAS),
∴CN=CM,∠BCN=∠ACM,
∴∠BCN+∠NCA=∠ACM+∠NCA,
∵∠ACB=90°,
∴∠NCM=90°,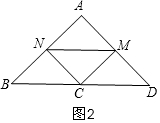
∴△NCM是等腰直角三角形,
即点M,N分别在线段AD,AB上,且AM=BN时,
△NCM是等腰直角三角形,
因此CM+CN的最小值时,就是MN取最小值,
当点M,N分别在线段AD,AB的中点时,MN最小,
如图2,∵M,N分别在线段AD,AB的中点,
∴MN是△ABD的中位线,
∴MN=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4,
∴CM=CN=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,
此时,CM+CN=2$\sqrt{2}$+2$\sqrt{2}$=4$\sqrt{2}$,
则CM+CN的最小值为4$\sqrt{2}$,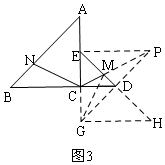
故答案为:4$\sqrt{2}$;
②如图3,由已知得:AC=BC=4,EC=DC=2,
延长EC至G,使EG=AC=4,过G作GH⊥AG,交ED的延长线于H,连接GD并延长至P,使GD=DP,连接EP、CP,CP交ED于M,连接GM,
则△ACB≌△EGH,此时CM+MG为最小,
∴AC=GH,AB=EH,∠A=∠H=45°,
∵BN=EM,
∴AN=HM,
∴△ANC≌△HMG,
∴CN=GM,
∴CM+MG=CM+CN,
∵CD∥GH,EC=CG,
∴ED=DH,
∵EG=GH,
∴GP⊥EH,
∴EH是PG的中垂线,
∴EG=EP,MG=PM,
∴∠EGP=∠EPG=45°,
∴∠GEP=90°,
∴CM+MG=CM+PM=PC,
在Rt△PEC中,由勾股定理得:PC=$\sqrt{P{E}^{2}+E{C}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴CM+CN=PC=2$\sqrt{5}$,
即则CM+CN的最小值为2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题是最短路线问题,考查了格点三角形、等腰直角三角形的性质和判定、轴对称的性质,第2问比较复杂,想办法通过辅助线将所求线段的和转化到同一个三角形内,利用作对称点的方法,才能使问题得以解决.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.
我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
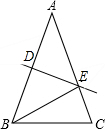 在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E.
在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD=$\frac{1}{2}$BC.
如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD=$\frac{1}{2}$BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com