
【题目】已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F.当BE=CF时,求证:AE=AF. 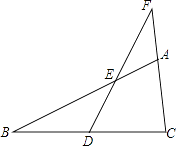
【答案】证明:过点B作BG∥FC,延长FD交BG于点G. 
∴∠G=∠F.
∵点D是BC的中点,
∴BD=CD.
在△BDG和△CDF中,
∴△BDG≌△CDF(AAS).
∴BG=CF.
∵BE=CF,
∴BE=BG.
∴∠G=∠BEG.
∵∠BEG=∠AEF,
∴∠G=∠AEF.
∴∠F=∠AEF.
∴AE=AF.
【解析】过点B作BG∥FC,延长FD交BG于点G.由平行线的性质可得∠G=∠F,然后判定△BDG和△CDF全等,根据全等三角形的性质和等量代换得到BE=BG,由等腰三角形的性质可得∠G=∠BEG,由对顶角相等及等量代换得出∠F=∠AEF,根据等腰三角形的判定得出AE=AF.
【考点精析】掌握平行线的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中画出钝角△ABC,使它的面积为6(画一个即可);
(2)在图2中画出△DEF,使它的三边长分别为![]() 、
、![]() 、5(画一个即可).并且直接写出此时三角形DEF的面积.
、5(画一个即可).并且直接写出此时三角形DEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0),C(﹣1,0). 
(1)将△ABC向右平移5个单位,再向下平移4个单位得△A1B1C1 , 图中画出△A1B1C1 , 平移后点A的对应点A1的坐标是 .
(2)将△ABC沿x轴翻折△A2BC,图中画出△A2BC,翻折后点A对应点A2坐标是 .
(3)将△ABC向左平移2个单位,则△ABC扫过的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:在等腰三角形ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边三角形ACE,直线BE交直线AD于点F,连接FC.
(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.
①求证:∠FEA=∠FCA;
②猜想线段FE,FA,FD之间的数量关系,并证明你的结论:
(2)当60°<∠BAC<120°,且△ACE与△ABC在直线AC的同侧时,利用图2画出图形探究线段FE,FA,FD之间的数量关系,并直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线y=﹣![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某花卉种植基地欲购进甲、乙两种君子兰进行培育,若购进甲种2株,乙种3株,则共需要成本1700元;若购进甲种3株,乙种1株,则共需要成本1500元.
(1)求甲乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购进甲、乙两种君子兰,若购进乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com