
【题目】(13分)如图所示,四边形![]() 中,
中, ![]() 于点
于点![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点。
上的一个动点。
(1)求证: ![]() 。
。
(2)过点![]() 分别作
分别作![]() 于
于![]() 点,作
点,作![]() 于
于![]() 点。
点。
① 试说明![]() 为定值。
为定值。
② 连结![]() ,试探索:在点
,试探索:在点![]() 运动过程中,是否存在点
运动过程中,是否存在点![]() ,使
,使![]() 的值最小。若存在,请求出该最小值;若不存在,请说明理由。
的值最小。若存在,请求出该最小值;若不存在,请说明理由。
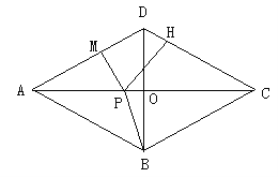
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:(1)由AC⊥BD,AO=CO,可知BD是AC的垂直平分线,由线段垂直平分线的性质可知AD=DC,AB=BC,同理可得AD=AB,CD=BC,故AB=BC=CD=AD;或先根据对角线互相平分的四边形是平行四边形先证四边形ABCD是平行四边形,然后根据对角线互相垂直的平行四边形是菱形证明四边形ABCD是菱形,进而得出结论;
(2)连接DP,根据题意可知: S△ADC=S△ADP+S△CDP,由三角形的面积公式可知: ![]() ACOD =
ACOD =![]() ADPM+
ADPM+![]() DCPH,将AC、OD、AD、DC的长代入化简即可;
DCPH,将AC、OD、AD、DC的长代入化简即可;
(3))由PM+PH为定值,当PB最短时,PM+PH+PB有最小值,由垂线的性质可知当点P与点O重合时,OB有最小值.
试题解析:
(1)证明:∵AO=CO,BD⊥AC,
∴AD=CD,AB=BC ,
同理可得AD=AB,CD=BC,
∴AB=BC=CD=AD;
另证:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形,
∴AB=BC=CD=AD.
(2)证明:∵AC⊥BD,BO=DO=5,AO=CO=12,
∴由勾股定理得AD=CD=13,
连结DP则S△ADC=S△ADP+S△CDP ,
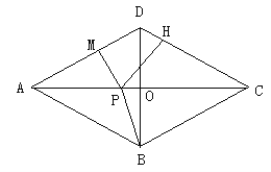
又∵PM⊥AD,PH⊥DC,DO⊥AC,
∴![]()
∴![]()
∴![]() 即
即![]() 为定值;
为定值;
(3)存在点![]() ,使
,使![]() 的值最小.
的值最小.
由(2)可知, ![]() 为定值
为定值
∴要使PM+PH+PB最小,则PB要取最小值
∵BO⊥AC,
∴当P与O重合时,PB最小,最小值为OB=5,
∴PM+PH+PB的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2 , 直线l和直线l1、l2分别交于点C和D,在直线l上有一点P(点P与点C,D不重合),点A在直线l1上,点B在直线l2上. 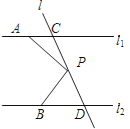
(1)当点P在C,D之间运动时,试说明:∠PAC+∠PBD=∠APB;
(2)当点P在直线l1的上方运动时,试探索∠PAC、∠APB、∠PBD之间的关系又是如何?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,2017年11月11日淘宝网一天的销售额为1682亿元,这个数据用科学记数法表示为( )
A. 1682×108 B. 16.82×1010 C. 1.682×1010 D. 1.682×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列去括号正确的是( )
A.﹣(a+b﹣c)=﹣a+b﹣c
B.﹣2(a+b﹣3c)=﹣2a﹣2b+6c
C.﹣(﹣a﹣b﹣c)=﹣a+b+c
D.﹣(a﹣b﹣c)=﹣a+b﹣c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com