
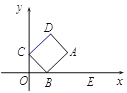
【题目】如图,矩形ABCD的顶点 A的坐标为(4,2),顶点B,C分别在![]() 轴,
轴,![]() 轴的正半轴上.
轴的正半轴上.
(1)求证:∠OCB=∠ABE;
(2)求OC长的取值范围;
(3)若D的坐标为(![]() ,
,![]() ),请说明
),请说明![]() 随
随![]() 的变化情况.
的变化情况.
【答案】(1)证明见解析;(2)0<OC≤2.(3)当0<![]() ≤2时,
≤2时,![]() 随
随![]() 的增大而增大;当2≤
的增大而增大;当2≤![]() <2时,
<2时,![]() 随
随![]() 的增大而减小.
的增大而减小.
【解析】试题分析:(1)根据矩形的性质得出∠CBA=∠COB=90°,求出∠OCB+∠CBO=90°,∠CBO+∠ABE=90°,即可得出答案;(2)过A作AF⊥x轴于F,证△COB∽△BEA,得出比例式,设OB=x,OC=y,则BE=4﹣x,求出y=﹣x2+2x=﹣![]() (x﹣2)2+2,即可得出答案;(3)求出n=﹣
(x﹣2)2+2,即可得出答案;(3)求出n=﹣![]() (m﹣2)2+4,根据二次函数的性质得出即可.
(m﹣2)2+4,根据二次函数的性质得出即可.
试题解析:
(1)证明:∵矩形ABCD,
∴∠ABC=90°,
∵∠BOC=90°,
∴∠ABC=∠BOC,
∵∠BOC+∠OCB=∠ABC+∠ABE,
∴∠OCB=∠ABE.
(2)解:过点A作AF⊥![]() 轴于F,
轴于F,
当点B在点F时,OC的长最小,为0.
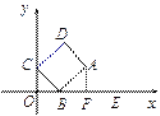
设OB=![]() ,OC=
,OC=![]() ,则BF=4-
,则BF=4-![]() .
.
∵AF⊥![]() 轴,
轴,
∴∠AFB=90°.
∴∠BOC=∠AFB=90°.
∴△BOC∽△AEB.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴OC的最大值为2.
∴OC的取值范围是0<OC≤2.
(3)解:过点D作AH⊥![]() 轴于H.
轴于H.
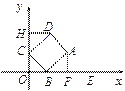
由矩形的性质易得△DHC≌△BFA.
∴DH=BF=4-![]() ,
,
CH=AF=2.
∴![]() ,
,![]() .
.
∴![]() .
.
∵0≤![]() <4,
<4,
∴0<![]() ≤4.
≤4.
∴当0<![]() ≤2时,
≤2时,![]() 随
随![]() 的增大而增大;当2≤
的增大而增大;当2≤![]() <2时,
<2时,![]() 随
随![]() 的增大而减小.
的增大而减小.


 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】下列对于随机事件的概率的描述:
①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”;
②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2;
③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85
其中合理的有______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一束光线从y轴的点A(0,2)出发,经过x轴上的点C反射后经过点B(6,6),则光线从点A到点B所经过的路程是( )
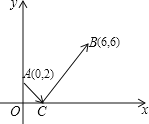
A.10B.8C.6D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
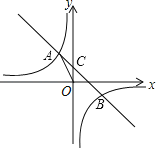
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=![]() (k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,3),点B与点A关于y=x成轴对称,tan∠AOC=
(k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,3),点B与点A关于y=x成轴对称,tan∠AOC=![]() .
.
(1)求k的值;
(2)直接写出点B的坐标,并求直线AB的解析式;
(3)P是y轴上一点,且S△PBC=2S△AOB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
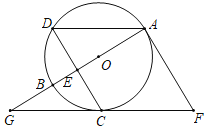
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是圆上一点,弦
是圆上一点,弦![]() 于点
于点![]() ,且
,且![]() .过点
.过点![]() 作
作![]() 的切线,过点
的切线,过点![]() 作
作![]() 的平行线,两直线交于点
的平行线,两直线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 与
与![]() 相切;
相切;
(2)连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 边上从点
边上从点![]() 运动到点
运动到点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,连
,连![]() ,在点
,在点![]() 运动过程中,请探究以下问题:
运动过程中,请探究以下问题:

(1)![]() 的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
(2)若![]() 为等腰三角形,求此时正方形
为等腰三角形,求此时正方形![]() 的边长.
的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于两个点
中,对于两个点![]() ,
,![]() 和图形
和图形![]() ,如果在图形
,如果在图形![]() 上存在点
上存在点![]() ,
,![]() (
(![]() ,
,![]() 可以重合),使得
可以重合),使得![]() ,那么称点
,那么称点![]() 与点
与点![]() 是图形
是图形![]() 的一对“倍点”.
的一对“倍点”.
已知![]() 的半径为1,点
的半径为1,点![]() .
.
(1)①点![]() 到
到![]() 的最大值,最小值;
的最大值,最小值;
②在![]() ,
,![]() ,
,![]() 这三个点中,与点
这三个点中,与点![]() 是
是![]() 的一对“倍点”的是_____;
的一对“倍点”的是_____;
(2)在直线![]() 上存在点
上存在点![]() 与点
与点![]() 是
是![]() 的一对“倍点”,求
的一对“倍点”,求![]() 的取值范围;
的取值范围;
(3)正方形![]() 的顶点
的顶点![]() ,
,![]() ,若正方形上的所有点与点
,若正方形上的所有点与点![]() 都是
都是![]() 的一对“倍点”,直接写出
的一对“倍点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应全民阅读的号召,某社区开展了为期一年的“读书伴我行”阅读活动,在阅读活动开展之初,随机抽取若干名社区居民,对其年阅读量(单位:本)进行了调查统计与分析,结果如下:
平均数 | 中位数 | 众数 | 最大值 | 最小值 | 方差 |
6.9 | 7.5 | 8 | 16 | 1 | 18.69 |
经过一年的“读书伴我行”阅读活动,某社区再次对这部分居民的年阅读量进行调查,并对收集的数据进行了整理、描述和分析,下面给出了部分信息.
a.居民的年阅读量统计表如下:
阅读量 | 2 | 4 | 5 | 8 | 9 | 10 | 11 | 12 | 13 | 16 | 21 |
人数 | 5 | 5 | 5 | 3 | 2 | m | 5 | 5 | 3 | 7 | n |
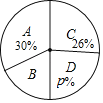
b.分组整理后的居民阅读量统计表、统计图如下:
组别 | 阅读量/本 | 频数 |
|
| 15 |
|
| |
|
| 13 |
|
|
c.居民阅读量的平均数、中位数、众数、最大值、最小值、方差如下:
平均数 | 中位数 | 众数 | 最大值 | 最小值 | 方差 |
10.4 | 10.5 | q | 21 | 2 | 30.83 |
根据以上信息,回答下列问题:
(1)样本容量为______;
(2)![]() _____;
_____;![]() _____;
_____;![]() ______;
______;
(3)根据社区开展“读书伴我行”阅读活动前、后随机抽取的部分居民阅读量的两组调查结果,请至少从两个方面对社区开展阅读活动的效果进行评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com