
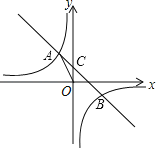
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=![]() (k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,3),点B与点A关于y=x成轴对称,tan∠AOC=
(k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,3),点B与点A关于y=x成轴对称,tan∠AOC=![]() .
.
(1)求k的值;
(2)直接写出点B的坐标,并求直线AB的解析式;
(3)P是y轴上一点,且S△PBC=2S△AOB,求点P的坐标.
【答案】(1)k=﹣3;(2)B(3,﹣1),直线AB的解析式为y=﹣x+2;(3)P点的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).
【解析】
(1)作AD⊥y轴于D,根据正切函数,可得AD的长,得到A的坐标,根据待定系数法,可得k的值;
(2)根据题意即可求得B点的坐标,然后根据待定系数法即可求得直线AB的解析式;
(3)先根据S△AOB=S△AOC+S△BOC求得△AOB的面积为4,然后设P(0,t),得出S△PBC=![]() |t﹣2|×3=
|t﹣2|×3=![]() |t﹣2|,由S△PBC=2S△AOB列出关于t的方程,解得即可.
|t﹣2|,由S△PBC=2S△AOB列出关于t的方程,解得即可.
解:(1)作AD⊥y轴于D,
∵点A的坐标为(m,3),
∴OD=3,
∵tan∠AOC=![]() .
.
∴![]() ,即
,即![]() ,
,
∴AD=1,
∴A(﹣1,3),
∵在反比例函数y=![]() (k为常数,k≠0)的图象上,
(k为常数,k≠0)的图象上,
∴k=﹣1×3=﹣3;
(2)∵点B与点A关于y=x成轴对称,
∴B(3,﹣1),
∵A、B在一次函数y=ax+b的图象上,
∴![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+2;
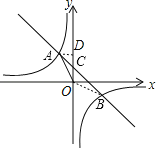
(3)连接OC,
由直线AB为y=﹣x+2可知,C(0,2),
∵S△AOB=S△AOC+S△BOC=![]() ×2×1+
×2×1+![]() ×2×3=4,
×2×3=4,
∵P是y轴上一点,
∴设P(0,t),
∴S△PBC=![]() |t﹣2|×3=
|t﹣2|×3=![]() |t﹣2|,
|t﹣2|,
∵S△PBC=2S△AOB,
∴![]() |t﹣2|=2×4,
|t﹣2|=2×4,
∴t=![]() 或t=﹣
或t=﹣![]() ,
,
∴P点的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.下面是小文的探究过程,请补充完整:
的图象与性质.下面是小文的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:

如图,在平面直角坐标系![]() 中,描出了以上表中各对应值为坐标的点.
中,描出了以上表中各对应值为坐标的点.
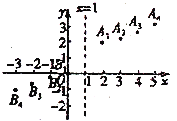
①观察图中各点的位置发现:点![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() 均关于某点中心对称,则该点的坐标为__________;
均关于某点中心对称,则该点的坐标为__________;
②小文分析函数![]() 表达式发现:当
表达式发现:当![]() 时,该函数的最大值为0,则该函数图象在直线
时,该函数的最大值为0,则该函数图象在直线![]() 左侧的最高点的坐标为__________;
左侧的最高点的坐标为__________;
(3)小文补充了该函数图象上两个点![]() ,
,![]() .
.
①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
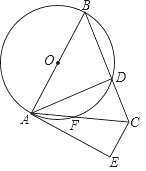
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE;
(2)若AB=10,AC=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名学生中选择一人参加电脑知识竞赛,在相同条件下对他们的电脑知识进行了10次测验,成绩如下:(单位:分)
甲成绩 | 76 | 84 | 90 | 84 | 81 | 87 | 88 | 81 | 85 | 84 |
乙成绩 | 82 | 86 | 87 | 90 | 79 | 81 | 93 | 90 | 74 | 78 |
(1)请完成下表:
| 平均数 | 中位数 | 众数 | 方差 | 85分以上的频率 |
甲 | 84 | 84 | 14.4 | 0.3 | |
乙 | 84 | 84 | 34 |
(2)利用以上信息,请从三个不同的角度对甲、乙两名同学的成绩进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
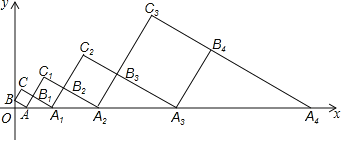
【题目】如图所示,在平面直角坐标系中,点A(![]() ,0)、B(0,
,0)、B(0,![]() ),以AB为边作正方形ABCB1,延长CB1交x轴于点A1,以A1B1为边作正方形A1B1C1B2,延长C1B2交x轴于点A2,以A2B2为边作正方形A2B2C2B3,延长C2B3交x轴于点A3,以A3B3为边作正方形A3B3C3B4,…,依此规律,则△A6B7A7的周长为_____.
),以AB为边作正方形ABCB1,延长CB1交x轴于点A1,以A1B1为边作正方形A1B1C1B2,延长C1B2交x轴于点A2,以A2B2为边作正方形A2B2C2B3,延长C2B3交x轴于点A3,以A3B3为边作正方形A3B3C3B4,…,依此规律,则△A6B7A7的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
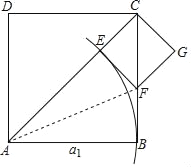
已知:如图,在正方形ABCD中,边AB=a1.
按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.
操作步骤 | 作法 | 由操作步骤推断(仅选取部分结论) |
第一步 | 在第一个正方形ABCD的对角线AC上截取AE=a1,再作EF⊥AC于点E,EF与边BC交于点F,记CE=a2 | (i)△EAF≌△BAF(判定依据是①); (ii)△CEF是等腰直角三角形; (iii)用含a1的式子表示a2为②: |
第二步 | 以CE为边构造第二个正方形CEFG; | |
第三步 | 在第二个正方形的对角线CF上截取FH=a2,再作IH⊥CF于点H,IH与边CE交于点I,记CH=a3: | (iv)用只含a1的式子表示a3为③: |
第四步 | 以CH为边构造第三个正方形CHIJ | |
这个过程可以不断进行下去.若第n个正方形的边长为an,用只含a1的式子表示an为④ | ||
请解决以下问题:
(1)完成表格中的填空:
① ;② ;③ ;④ ;
(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ(不要求尺规作图).
查看答案和解析>>
科目:初中数学 来源: 题型:
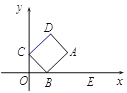
【题目】如图,矩形ABCD的顶点 A的坐标为(4,2),顶点B,C分别在![]() 轴,
轴,![]() 轴的正半轴上.
轴的正半轴上.
(1)求证:∠OCB=∠ABE;
(2)求OC长的取值范围;
(3)若D的坐标为(![]() ,
,![]() ),请说明
),请说明![]() 随
随![]() 的变化情况.
的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
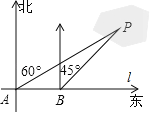
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
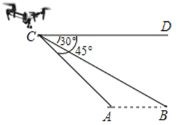
【题目】为开发大西北,某工程队承接高铁修筑任务,在山坡处需要修建隧道,为了测量隧道的长度,工程队用无人机在距地面高度为500米的C处测得山坡南北两端A、B的俯角分别为∠DCA=45°、∠DCB=30°(已知A、B、C三点在同一平面上),求隧道两端A、B的距离.(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com