
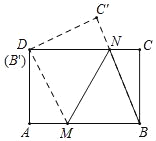
【题目】如图,四边形ABCD为矩形,将矩形ABCD沿MN折叠,折痕为MN,点B的对应点B′落在AD边上,已知AB=6,AD=4.
(1)若点B′与点D重合,连结DM,BN,求证:四边形BMB′N为菱形;
(2)在(1)问条件下求出折痕MN的长.
【答案】(1)证明见解析;(2)MN=![]() .
.
【解析】
(1)首先证明四边形BMDN是平行四边形,再证明BM=DM,即可证明四边形BMB'N为菱形.(2)首先设BM=x,利用在Rt△AMB′中,结合勾股定理,求解x的值,在计算NQ,在Rt△MNQ中,利用勾股定理,即可得MN的长.
解:(1)由折叠可得,BM=DM,∠BMN=∠DMN,
∵CD∥AB,
∴∠BMN=∠DNM,
∴∠DMN=∠DNM,
∴DN=DM,
∴BM=MD=DN,
又∵DN∥BM,
∴四边形BMDN是平行四边形,
又∵BM=DM,
∴四边形BMB'N为菱形;
(2)设BM=x,则DM=x,AM=6﹣x,
在Rt△AMB′中,由勾股定理可得,(6﹣x)2+42=x2,
求解得x=![]() ,
,
则DM=![]() =DN,
=DN,
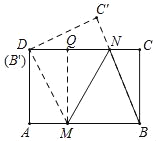
如图,过点M作MQ⊥CD于点Q,则
NQ=![]() -(6-
-(6-![]() )=
)=![]() ,
,
在Rt△MNQ中,利用勾股定理可得MN=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】学校新到一批理、化、生实验器材需要整理,若实验管理员李老师一人单独整理需要40分钟完成,现在李老师与工人王师傅共同整理20分钟后,李老师因事外出,王师傅再单独整理了20分钟才完成任务.
(1)王师傅单独整理这批实验器材需要多少分钟?
(2)学校要求王师傅的工作时间不能超过30分钟,要完成整理这批器材,李老师至少要工作多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
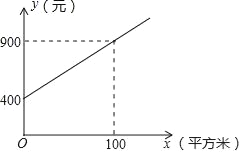
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江津区某玩具商城在“六一”儿童节来临之际,以49元/个的价格购进某种玩具进行销售,并预计当售价为50元/个时,每天能售出50个玩具,且在一定范围内,当每个玩具的售价平均每提高0.5元时,每天就会少售出3个玩具。
(1)若玩具售价不超过60元/个,每天售出玩具总成本不高于686元,预计每个玩具售价的取值范围;
(2)在实际销售中,玩具城以(1)中每个玩具的最低售价及相应的销量为基础,进一步调整了销售方案,将每个玩具的售价提高了![]() %,从而每天的销售量降低了
%,从而每天的销售量降低了![]() %,当每天的销售利润为147元时,求a的值.
%,当每天的销售利润为147元时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=![]() +bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,
+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,![]() )、点B(
)、点B(![]() ,
,![]() )、点C(
)、点C(![]() ,
,![]() )在该函数图象上,则
)在该函数图象上,则![]() <
<![]() <
<![]() ;(5)若方程a(x+1)(x﹣5)=﹣3的两根为
;(5)若方程a(x+1)(x﹣5)=﹣3的两根为![]() 和
和![]() ,且
,且![]() <
<![]() ,则
,则![]() <﹣1<5<
<﹣1<5<![]() .其中正确的结论有( ).
.其中正确的结论有( ).

A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
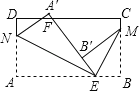
【题目】如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)判断直线EN,ME的位置关系,并说明理由;
(2)设∠MEN的平分线EP交边CD于点P,∠MEN的一条三等分线EQ交边CD于点Q.求∠PEQ的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )

A. (6,0) B. (6,3) C. (6,5) D. (4,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com