
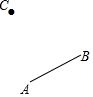
 已知AB是⊙O的弦,点C为圆上一点.
已知AB是⊙O的弦,点C为圆上一点.分析 (1)连结AC,分别作AB、AC的中垂线,交点即为圆心O,然后以O为圆心,OA为半径作圆即可;
(2)AB的中垂线与⊙O交点分别为E1、E2,△ABE1与△ABE2均为以AB为底的圆的内接等腰三角形;
(3)由R=5,AB=8,根据勾股定理易得AB对应的弦心距为3,进而得到h=5+3=8或h=5-3=2.
解答 解:(1)如图所示,连结AC,分别作AB、AC的中垂线,交点即为圆心O,然后以O为圆心,OA为半径作圆即可;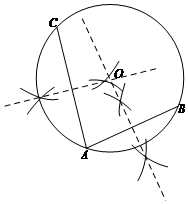
(2)如图所示,若AB的中垂线与⊙O交点分别为E1、E2,
则△ABE1与△ABE2均为以AB为底的圆的内接等腰三角形;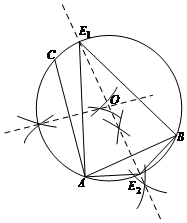
(3)由圆的半径R=5,AB=8,由勾股定理可得AB对应的弦心距为3,
∴△ABE1中,h=5+3=8;
△ABE2中,h=5-3=2.
点评 本题主要考查了等腰三角形的性质,三角形的外接圆与外心的运用,解决问题时注意:找一个三角形的外心,就是找一个三角形的两条边的垂直平分线的交点,三角形的外接圆只有一个.


科目:初中数学 来源: 题型:选择题
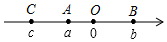 如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
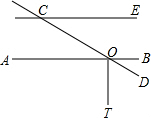
| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:填空题
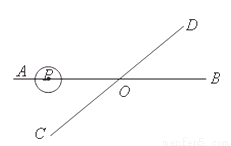
如图,直线AB、CD相交于点O,∠AOC=300,半径为1cm的⊙P的圆心在射线OA上,开始时,PO=6cm.如果⊙P以1cm/秒的速度沿由A向B的方向移动,那么当⊙P的运动时间t(秒)满足条件____________时,⊙P与直线CD相交.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com