
分析 (1)根据应缴水费=2×用水量+0.80×用水量,代入数据即可求出结论;
(2)根据应缴水费=2×20+超出20吨的部分×a+0.80×用水量即可得出关于a的一元一次方程,解之即可得出a值;
(3)设该用户该月的用水量为x吨,根据应缴水费=2×20+超出20吨的部分×3+0.80×用水量即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)15×2+15×0.80=42(元).
故答案为:42.
(2)根据题意得:20×2+(30-20)a+30×0.80=94,
解得:a=3.
答:a的值为3.
(3)设该用户该月的用水量为x吨,
根据题意得:20×2+3(x-20)+0.80x=151,
解得:x=45.
答:该用户该月的用水量为45吨.
点评 本题考查了一元一次方程的应用,解题的关键是:(1)根据应缴水费=2×用水量+0.80×用水量列式计算;(2)根据应缴水费=2×20+超出20吨的部分×a+0.80×用水量列出关于a的一元一次方程;(3)根据应缴水费=2×20+超出20吨的部分×3+0.80×用水量列出关于x的一元一次方程.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
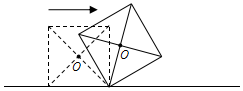 如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )
如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )| A. | 4a | B. | 2$\sqrt{2}$πa | C. | $\sqrt{2}$πa | D. | $\sqrt{2}$a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
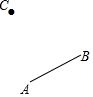 已知AB是⊙O的弦,点C为圆上一点.
已知AB是⊙O的弦,点C为圆上一点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:单选题
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为 ,较长直角边为
,较长直角边为 ,那么
,那么 的值为( )
的值为( )
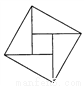
A. 13 B. 19 C. 25 D. 169
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com