
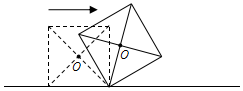
 如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )
如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )| A. | 4a | B. | 2$\sqrt{2}$πa | C. | $\sqrt{2}$πa | D. | $\sqrt{2}$a |
分析 根据正方形的性质易得OC=$\frac{\sqrt{2}}{2}$a,∠OCO′=90°,又边长为a的正方形ABCD沿直线l向右做无滑动地翻滚,当正方形翻滚一周时,需要翻滚四次,而每次正方形的中心O所经过的路径长为弧OO′(以C为圆心,OC为半径),然后根据弧长公式计算出弧OO′的长,再乘以4即可.
解答 解:如图
∵四边形ABCD为正方形,且边长为a,
∴OC=$\frac{\sqrt{2}}{2}$a,∠OCO′=90°,
∵边长为a的正方形ABCD沿直线l向右做无滑动地翻滚,当正方形翻滚一周时,需要翻滚四次,
而每次正方形的中心O所经过的路径长为弧OO′(以C为圆心,OC为半径),
∴弧OO′的长=$\frac{90π•\frac{\sqrt{2}}{2}a}{180}$=$\frac{\sqrt{2}}{4}$aπ,
∴当正方形翻滚一周时,正方形的中心O所经过的路径长=4×$\frac{\sqrt{2}}{4}$aπ=$\sqrt{2}$aπ.
故选C.
点评 本题考查了弧长公式:l=$\frac{nπr}{180}$(n为弧所对的圆心角,R为半径).也考查了正方形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
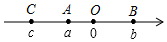 如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图为某地区今年4月的均气温频数直方图(直方图中每一组包括前一个边界值,不包括后一个边界值),则在下列结论中:
如图为某地区今年4月的均气温频数直方图(直方图中每一组包括前一个边界值,不包括后一个边界值),则在下列结论中:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
我市某工艺厂为配合伦敦奥运,设计了一款成本为20元/件的工艺品投入市场进行试销,得到如下数据:
销售单价x (元/件) | …… | 30 | 40 | 50 | 60 | …… |
每天销售量y(件) | …… | 500 | 400 | 300 | 200 | …… |
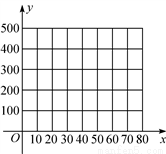
(1)把上表中x、y的各组对应值作为点的坐标,在右面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为9000元?
(利润=销售总价-成本总价)
(3)根据要求,试销该工艺品每天获得的利润不低于8000元,每天销售量不低于350件,试确定销售单价x(元/件)的取值范围,并求出工艺厂试销该工艺品每天获得的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com