
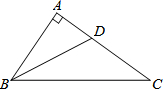
 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AB=6,BC=10,则AD为3.
如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AB=6,BC=10,则AD为3. 分析 根据勾股定理得到AC=8,过D作DE⊥BC于E,由角平分线的性质得到AD=DE,根据全等三角形的性质得到BE=AB=6,求得CE=4,根据勾股定理列方程即可得到结论.
解答 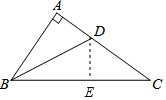 解:∵∠A=90°,AB=6,BC=10,
解:∵∠A=90°,AB=6,BC=10,
∴AC=8,
过D作DE⊥BC于E,
∵∠A=90°,∠ABC的平分线BD交AC于点D,
∴AD=DE,
在Rt△ABD与Rt△EBD中$\left\{\begin{array}{l}{AD=DE}\\{BD=BD}\end{array}\right.$,
∴Rt△ABD≌Rt△EBD,
∴BE=AB=6,
∴CE=4,
∴DE2+CE2=CD2,
即AD2+42=(8-AD)2,
∴AD=3,
故答案为:3.
点评 本题考查了勾股定理,全等三角形的判定和性质,角平分线的性质,正确的作出辅助线是解题的关键.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:选择题
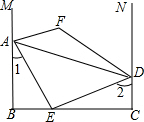 如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:
如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
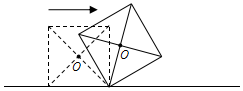 如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )
如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )| A. | 4a | B. | 2$\sqrt{2}$πa | C. | $\sqrt{2}$πa | D. | $\sqrt{2}$a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
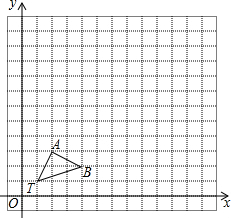 在12×12的正方形网格中,△TAB的顶点坐标为T(1,1)、A(2,3)、B(4,2)
在12×12的正方形网格中,△TAB的顶点坐标为T(1,1)、A(2,3)、B(4,2)查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
学校为了响应国家阳光体育活动,选派部分学生参加足球、乒乓球、篮球、排球队集训.根据参加项目制成如下两幅不完整的统计图(要求每位同学只能选择一种自己喜欢的球类,图中用足球、乒乓球、篮球、排球代表喜欢这四种球类某种球类的学生人数,请你根据图中提供的信息解答下列问题:
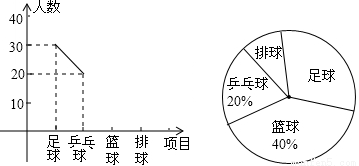
(1)参加篮球队的有 人,参加足球队的人数占全部参加人数的 %.
(2)喜欢排球队的人数在扇形统计图中所占的圆心角是多少度?并补全频数分布折线统计图.
(3)若足球队只剩一个集训名额,学生小明和小虎都想参加足球队,决定采用随机摸球的方式确定参加权,具体规则如下:一个不透明的袋子中装着标有数字1、2、3、4的四个完全相同的小球,小明随机地从四个小球中摸出一球然后放回,小虎再随机地摸出一球,若小明摸出的小球标有数字比小虎摸出的小球标有的数字大,则小明参加;若小明摸出的小球标有数字比小虎摸出的小球标有的数字小,则小虎参加,试分析这种规则对双方是否公平?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com